Hierarchical and Density Based Clustering
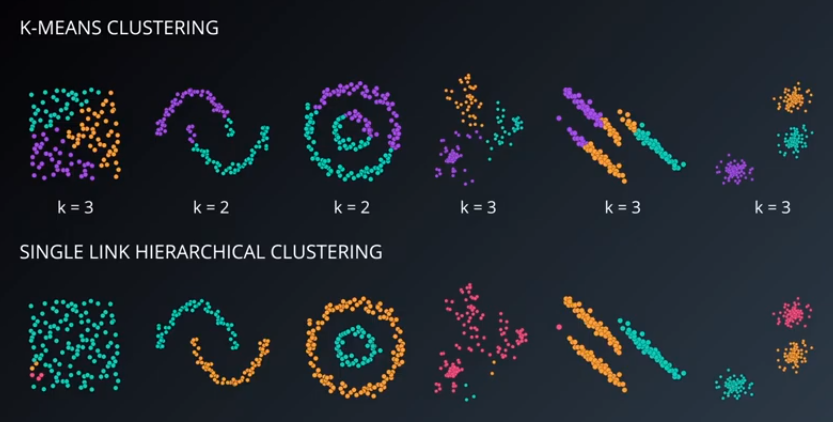
K-Means is a great algorithm for certain specific cases that rely on distance from a centroid as a definition for a cluster. K-Means always tries to find clusters that are circular, spherical, or hyper-spherical in higher dimensions. K-Means will not find more complexly-shaped clusters, such as those shown below.

The two new algorithms this section introduces are hierarchical clustering and density clustering. Hierarchical clustering gives a visual indication of how clusters relate to each other, as shown in the image below.

Density clustering, specifically the DBSCAN (“Density-Based Clustering of Applications with Noise”) algorithm, clusters points that are densely packed together and labels the other points as noise. It performs particularly well on the two-crescent dataset.

Hierarchical Clustering
Single-Link clustering is a specific type of hierarchical clustering. The algorithm is:
- Choose the nearest two points and form a cluster. If two clusters or a point and a cluster are the nearest two items, then consider the location of the cluster to be the location of the nearest point in that cluster. This is called the distance measure of the algorithm.
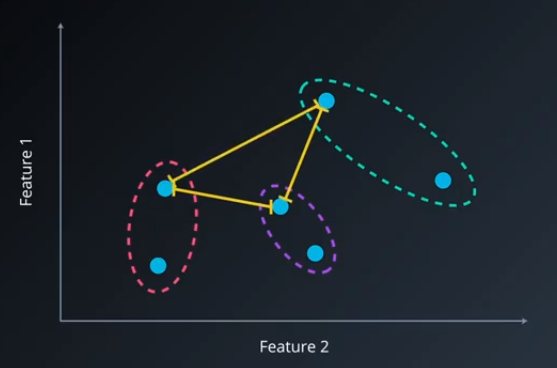
- Repeat step 1 until all points and clusters have been clustered together. The resulting hierarchical structure is called a "dendrogram."

- Depending on the number of clusters that are needed, eliminate the top few clusters in the dedrogram. Values from one to the number of samples will be possible.

The thing that separates a lot of the hierachical clustering methods is what to consider the location of the clusters, when clusters are joined. As mentioned above, for single-link clustering, the location is the nearest point. This way of creating clusters means that clusters can become very elongated and can eat up most of the dataset.

Complete Link, Average Link, and Ward
Single-link clustering is not included in Scikit, but three other types of agglomerative clustering are. Agglomerative clustering is a specific type of hierarchical clustering that builds clusters from the bottom, up.
Complete-Link clustering uses a different distance measure than Single-Link. Instead of distances between clusters being the distance to the nearest point, complete-link looks at the farthest two points in the two clusters. A distance measure like this produces compact clusters, which are generally considered better.
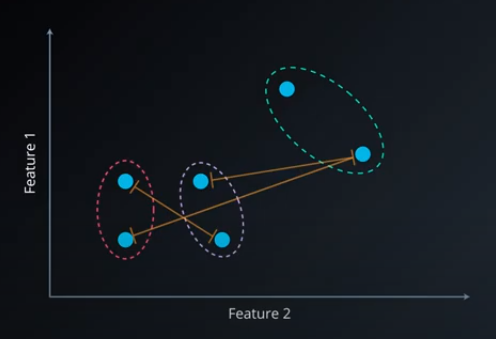
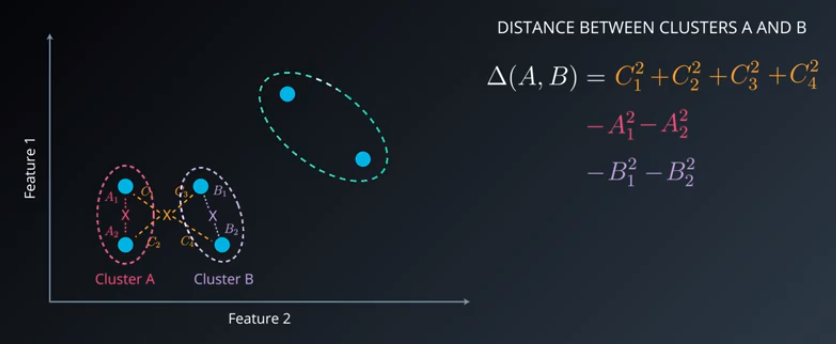
Average-Link looks at the average distance between every point and every other point.

Ward’s Method is the default method in Scikit for hierarchical clusters. It tries to minimize variance when merging two clusters.
Hierarchical Clustering Advantages
- Resulting hierarchical representation can be very informative
- Provides and additional ability to visualize
- Especially potent when the dataset contains real hierarchical relationships (think of biology)
Hierarchical Clustering Disadvantages
- Sensitive to noise and outliers
- Computationally intensive $O(N^2)$
DBSCAN
DBSCAN stands for “Density-Based Spatial Clustering of Applications with Noise.” Here is a link to a tool to visualize how DBSCAN works.
DBSCAN groups together closely-packed points. The most stark difference between DBSCAN and other clustering algorithms is that not every point is part of a cluster; these points are considered noise. Other points are classified as either a core point or border point.
There are two inputs to DBSCAN:
- $\epsilon$, the search distance around point, and
- $minpts$, the minimum number of points required to form a density cluster
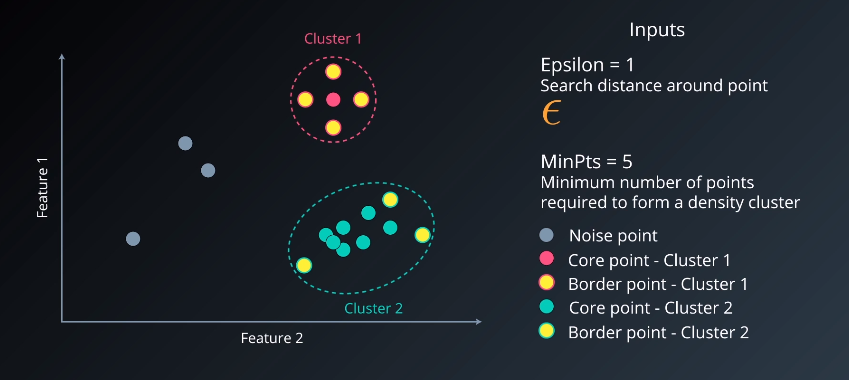
Note that cluster 1 is compact but cluster 2 may continue to be elongated and not necessarily compact.

DBSCAN Examples and Applications
Advantages
- We don’t need to specify the number of clusters
- Flexibility in the shapes & sizes of clusters
- Able to deal with noise and outliers
Disadvantages
- Border points that are reachable from two clusters may be arbitrarily classified - not an issue for most datasets
- Faces difficulty finding clusters of varying densities - to solve for this, can use a variation of DBSCAN called HDBSCAN
Two examples of applications for DBSCAN are linked below.