Gaussian Mixture Model Examples
1. KMeans versus GMM on a Generated Dataset
Use sklearn’s make_blobs function to create a dataset of Gaussian blobs.
import numpy as np
import matplotlib.pyplot as plt
from sklearn import cluster, datasets, mixture
%matplotlib inline
n_samples = 1000
varied = datasets.make_blobs(n_samples=n_samples,
cluster_std=[5, 1, 0.5],
random_state=3)
X, y = varied[0], varied[1]
plt.figure(figsize=(16,12))
plt.scatter(X[:,0], X[:,1],
c=y, edgecolor='black', lw=1.5,
s=100, cmap=plt.get_cmap('viridis'))
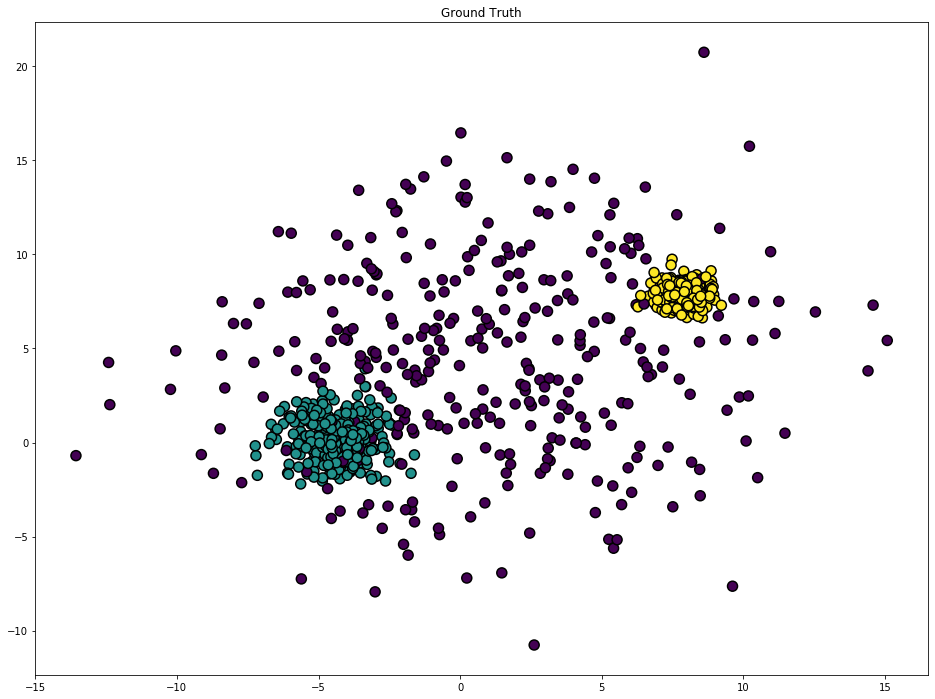
plt.title('Ground Truth')
plt.show()
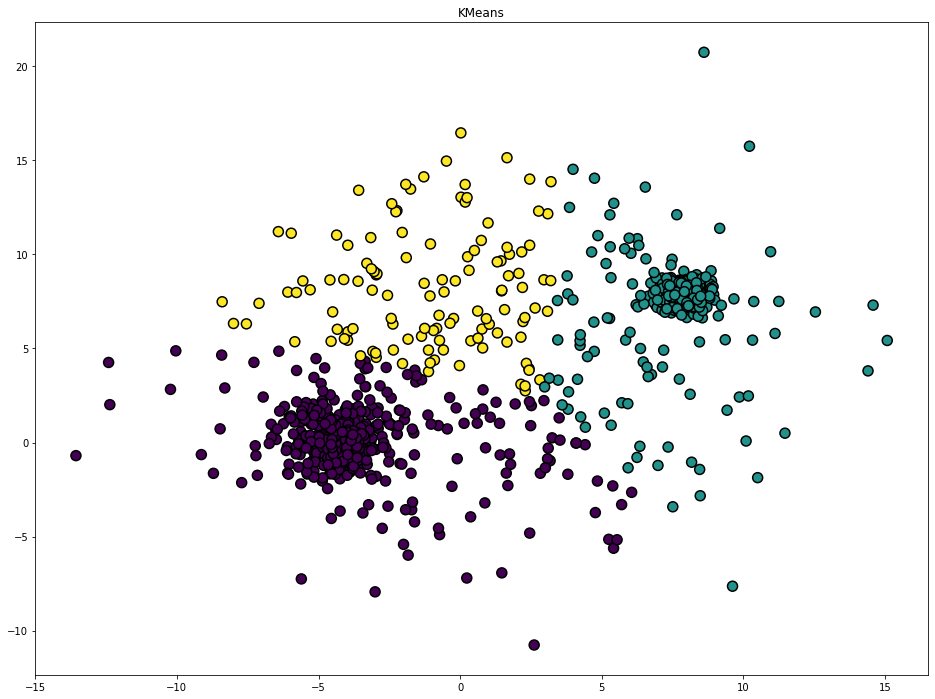
KMeans
from sklearn.cluster import KMeans
kmeans = KMeans(n_clusters=3)
pred = kmeans.fit_predict(X)
plt.figure( figsize=(16,12))
plt.scatter(X[:,0], X[:,1],
c=pred, edgecolor='black', lw=1.5,
s=100, cmap=plt.get_cmap('viridis'))
plt.title('KMeans')
plt.show()
GuassianMixture
from sklearn.mixture import GaussianMixture
gmm = GaussianMixture(n_components=3).fit(X)
gmm = gmm.fit(X)
pred_gmm = gmm.predict(X)
plt.figure( figsize=(16,12))
plt.scatter(X[:,0], X[:,1], c=pred_gmm, edgecolor='black', lw=1.5, s=100, cmap=plt.get_cmap('viridis'))
plt.show()
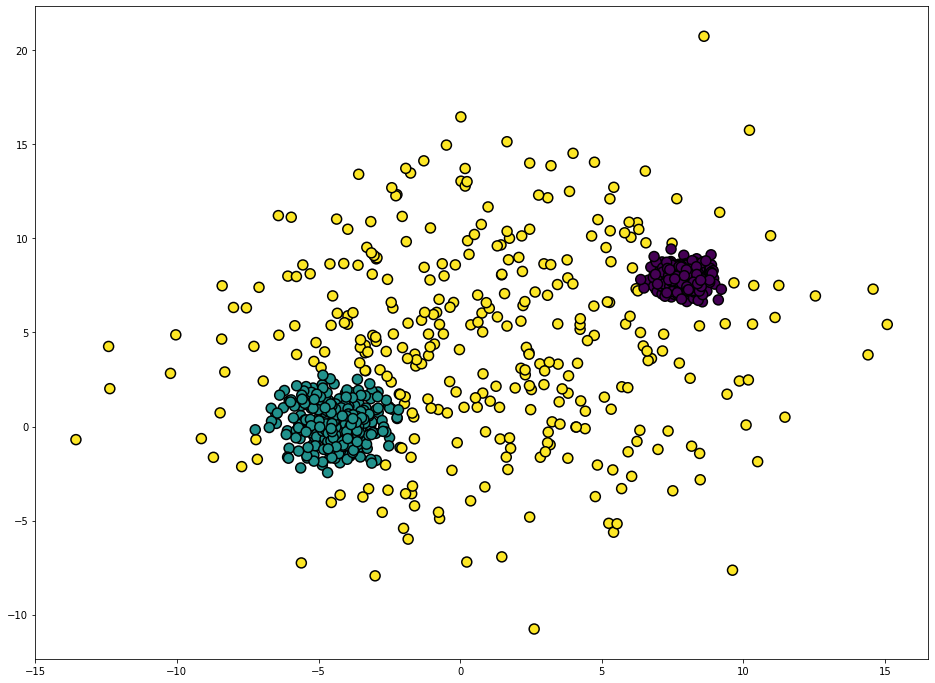
GaussianMixture clearly outperforms Kmeans on this dataset. This is expected since make_blobs creates Gaussian blobs.
2. KMeans versus GMM on the Iris Dataset
For the second example, use the Iris dataset. The Iris Dataset is great for this purpose since it is likely the data is normally-distributed.
import seaborn as sns
iris = sns.load_dataset("iris")
iris.info()
iris.head()
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 150 entries, 0 to 149
Data columns (total 5 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 sepal_length 150 non-null float64
1 sepal_width 150 non-null float64
2 petal_length 150 non-null float64
3 petal_width 150 non-null float64
4 species 150 non-null object
dtypes: float64(4), object(1)
memory usage: 6.0+ KB
| sepal_length | sepal_width | petal_length | petal_width | species | |
|---|---|---|---|---|---|
| 0 | 5.1 | 3.5 | 1.4 | 0.2 | setosa |
| 1 | 4.9 | 3.0 | 1.4 | 0.2 | setosa |
| 2 | 4.7 | 3.2 | 1.3 | 0.2 | setosa |
| 3 | 4.6 | 3.1 | 1.5 | 0.2 | setosa |
| 4 | 5.0 | 3.6 | 1.4 | 0.2 | setosa |
There are several ways to visualize a dataset with four dimensions, such as:
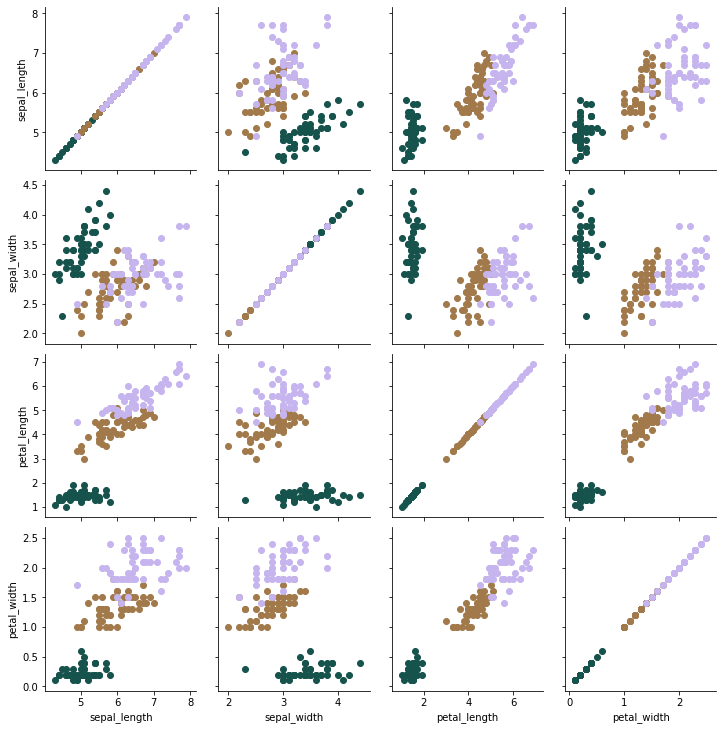
Use PairGrid since it does not distort the dataset. It simply plots every pair of features against each other in a subplot.
g = sns.PairGrid(iris, hue="species",
palette=sns.color_palette("cubehelix", 3),
vars=['sepal_length','sepal_width',
'petal_length','petal_width'])
g.map(plt.scatter)
plt.show()
kmeans_iris = KMeans(n_clusters=3)
pred_kmeans_iris = kmeans_iris.fit_predict(iris[['sepal_length',
'sepal_width',
'petal_length',
'petal_width']])
iris['kmeans_pred'] = pred_kmeans_iris
g = sns.PairGrid(iris, hue="kmeans_pred",
palette=sns.color_palette("cubehelix", 3),
vars=['sepal_length','sepal_width',
'petal_length','petal_width'])
g.map(plt.scatter)
plt.show()
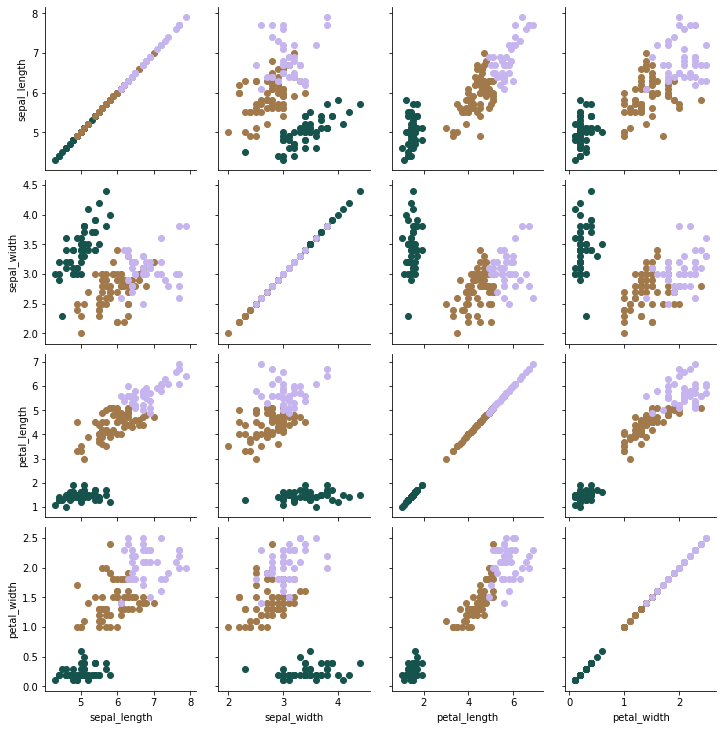
Visual inspection is no longer useful since we are working with multiple dimensions. Instead, use the adjusted Rand score which generates a score betwen -1 and 1, where an exact match would be scored as a 1.
from sklearn.metrics import adjusted_rand_score
iris_kmeans_score = adjusted_rand_score(iris['species'],
iris['kmeans_pred'])
round(iris_kmeans_score,3)
0.73
Now, try with Gaussian Mixture models.
gmm_iris = GaussianMixture(n_components=3).fit(iris[['sepal_length',
'sepal_width',
'petal_length',
'petal_width']])
pred_gmm_iris = gmm_iris.predict(iris[['sepal_length',
'sepal_width',
'petal_length',
'petal_width']])
iris['gmm_pred'] = pred_gmm_iris
iris_gmm_score = adjusted_rand_score(iris['species'],
iris['gmm_pred'])
round(iris_gmm_score,3)
0.904
The Gaussian Mixture model outperforms KMeans according to the ARI scores.