Model Evaluation
Evaluating some dataset and using it to make predictions is the problem we are trying to solve. The tools at our disposal are the various models and algorithms available to perform the actual machine learning: linear and logistic regression, SVMs, decision trees, neural networks, etc. Our measurement tools are used to determine which of the tools performs best on this particular problem. Once we determine which tool is the best for the task at hand, we can use it to solve the problem. This section discusses the various measurement tools at our disposal.

Or, more directly:
This section focuses on two questions:
- How well is the model doing?
- Specifically, is the model good or not? Are there metrics we can use to make this determination?
- How do we improve the model based on these metrics?
Testing Models
Recall that regression models predict a numeric value, whereas classification models predict a state.
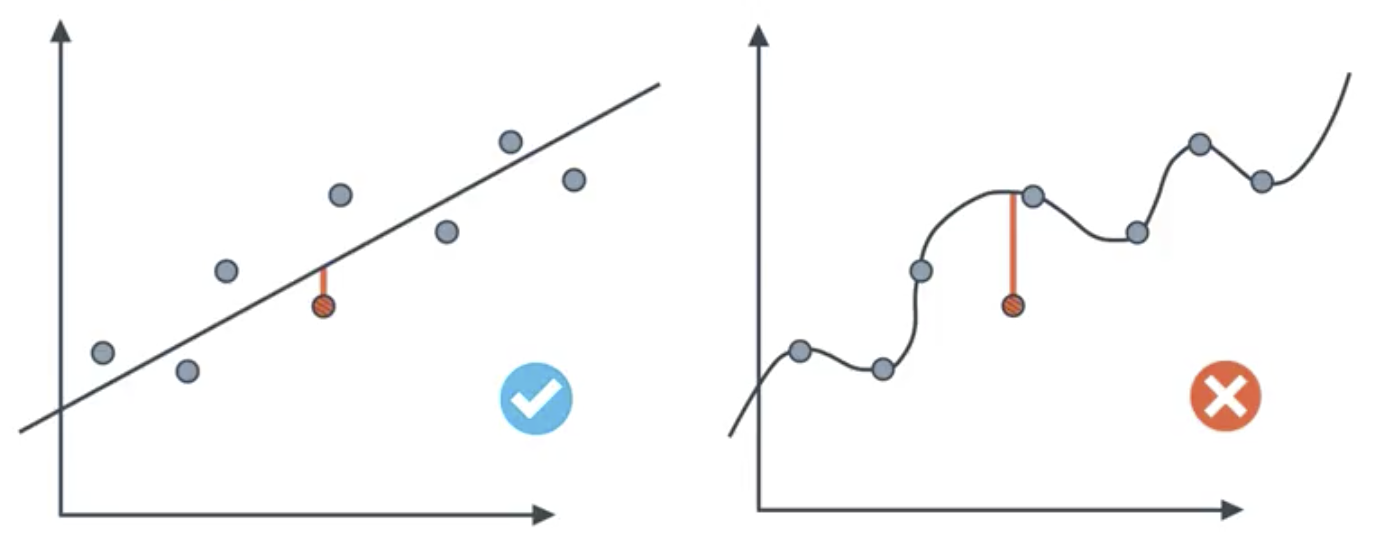
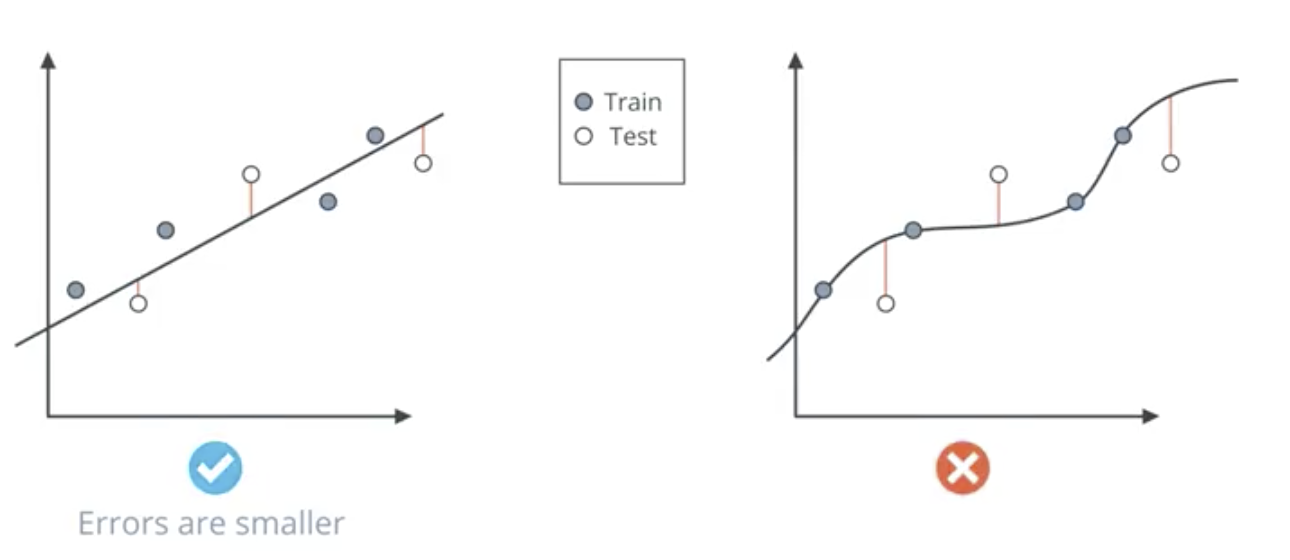
The model on the left fits the data well and will generalize to new data. The model on the right is clearly overfit. Testing is the means by which we determine whether the model is well-fit to the data. Specifically, this entails splitting the dataset into testing and training sets.
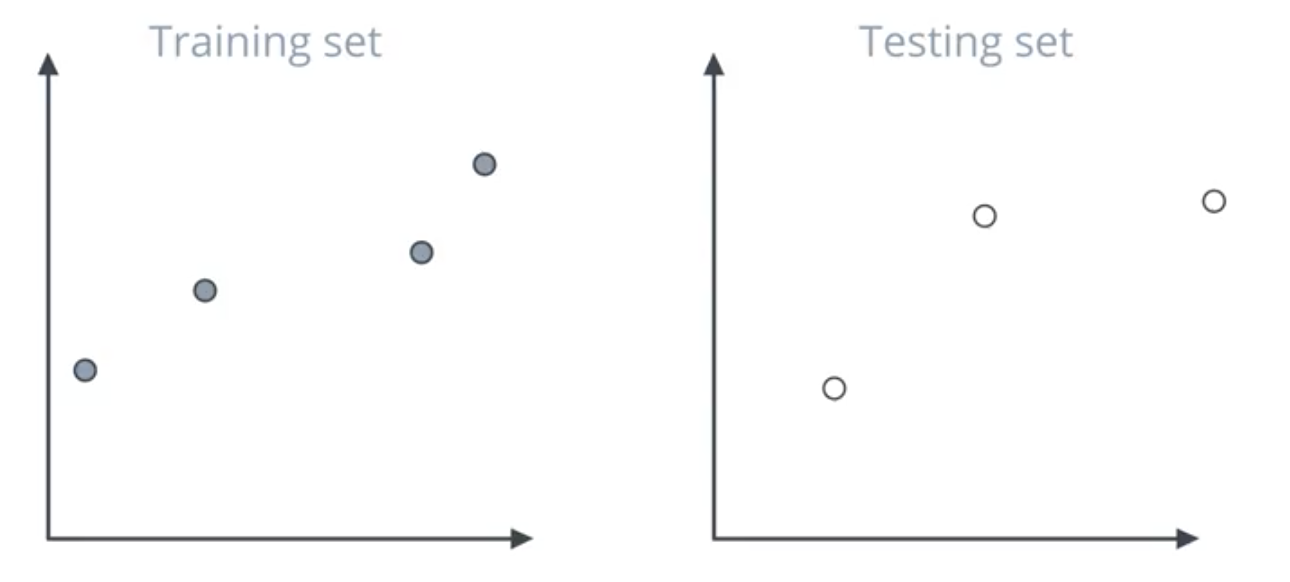
In the image below, though the model on the left performs worse on the grey training set, it performs better on the white testing set.
The case is similar for classification models, where the line is the boundary between the two classes.
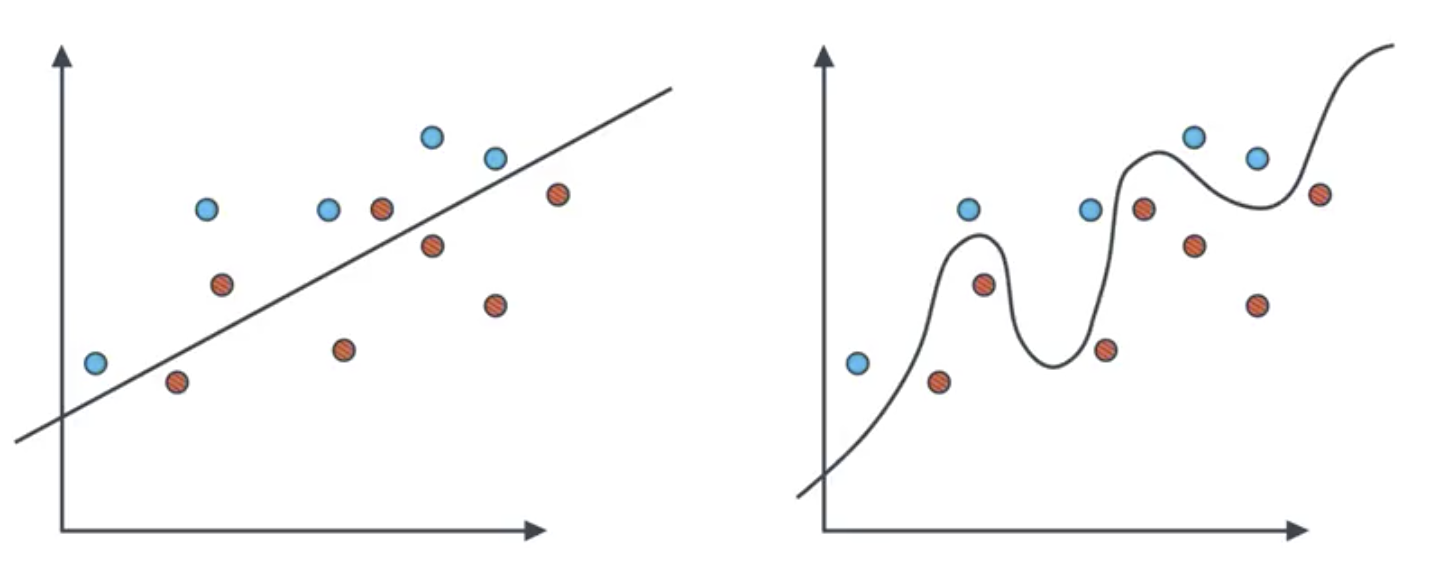
Note that in the image below, the overfit model on the right makes two classification errors, where as the model on the left only makes one.
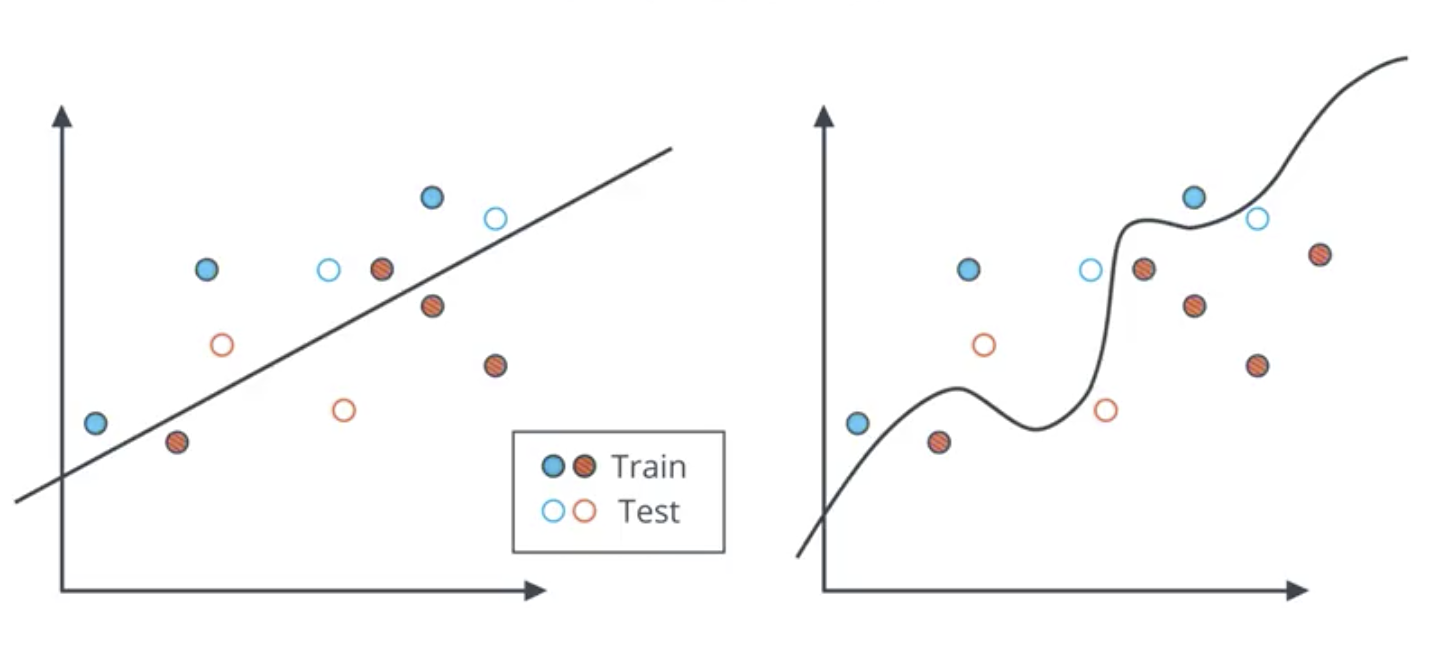
The sklearn train_test_split mtool is used to split a single dataset into training and testing sets. The hyperparameter test_size is used to control the proportion of the data that is used for the test set. So, if the dataset is 16 points and the test_size = .25, 4 of them would be used for the test set. The test set is to never be used for training.
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, t_test = train_test_split(X,
y,
test_size = 0.25)
Confusion Matrix
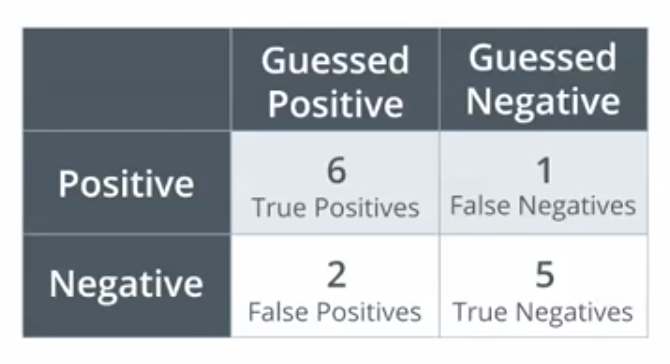
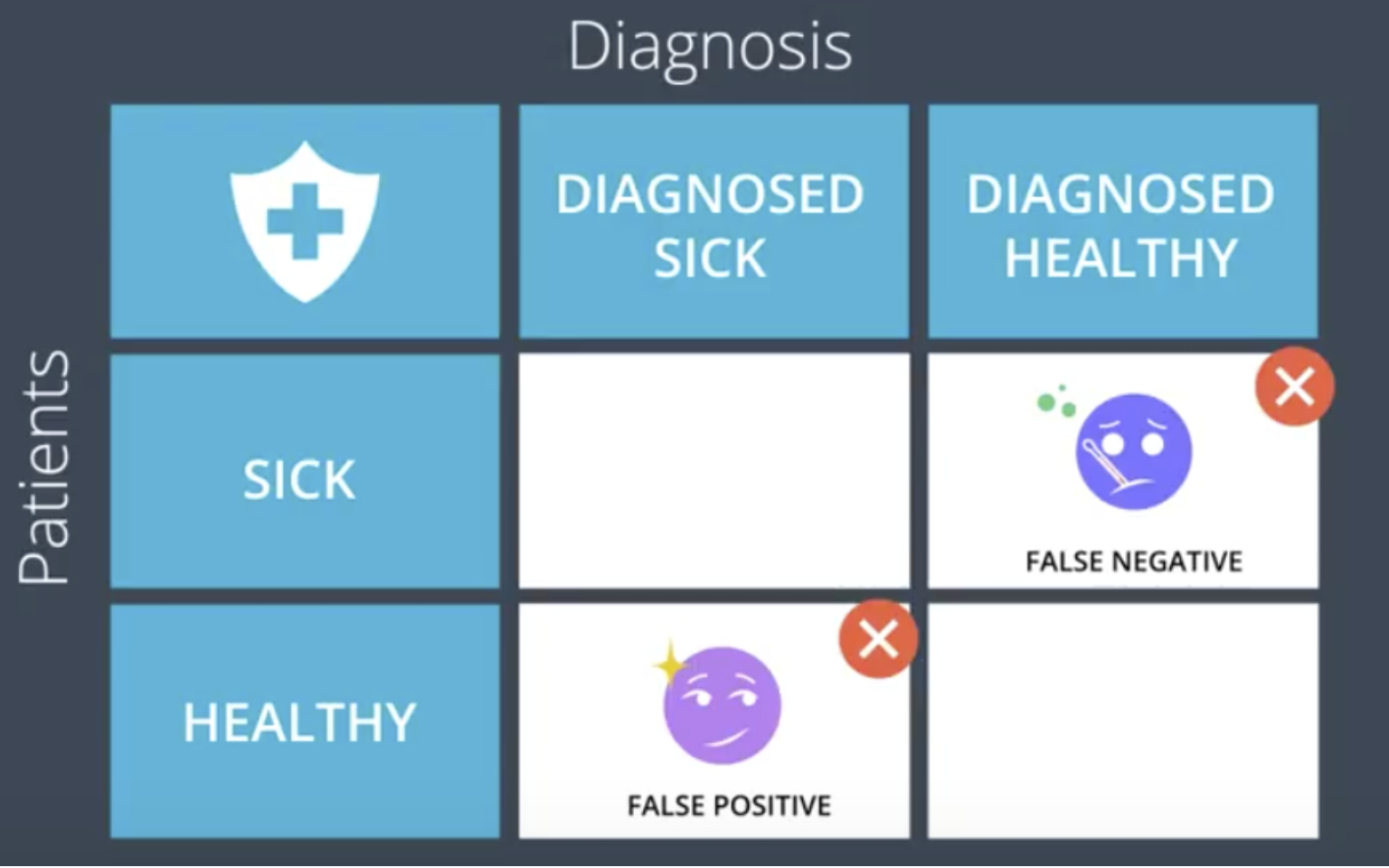
To determine if a model is performing well or not, it is necessary to consider the type of model it is as well as the type of error it is making. A medical model that is used for determining whether or not a patient is sick would have different performance requirements than a model for classifying spam email, for example. In either case, the “false negative” (or “Type 1 Error,” or “Error of the first kind”) situation is undesirable. In the medical case, this would mean misdiagnosing a sick patient as healthy. In the email case, this would mean classifying a piece of spam as a normal email and sending it to the person’s inbox. Obviously, there are much higher risks associated with false negatives in the medical model.
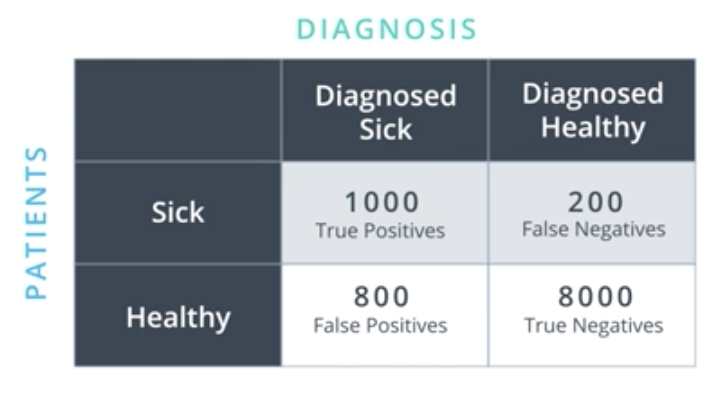
To capture and account for these different types of errors, we use the confusion matrix, shown below for the medical case.
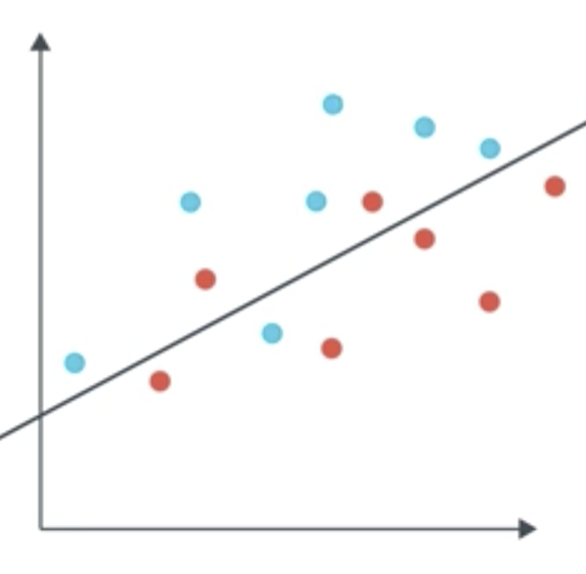
The generic confusion matrix is shown below, alongside a classification model used to generate the results below the table. The blue points are labelled positive; the red points, negative. The points above the line are predicted positive; the points below, negative.
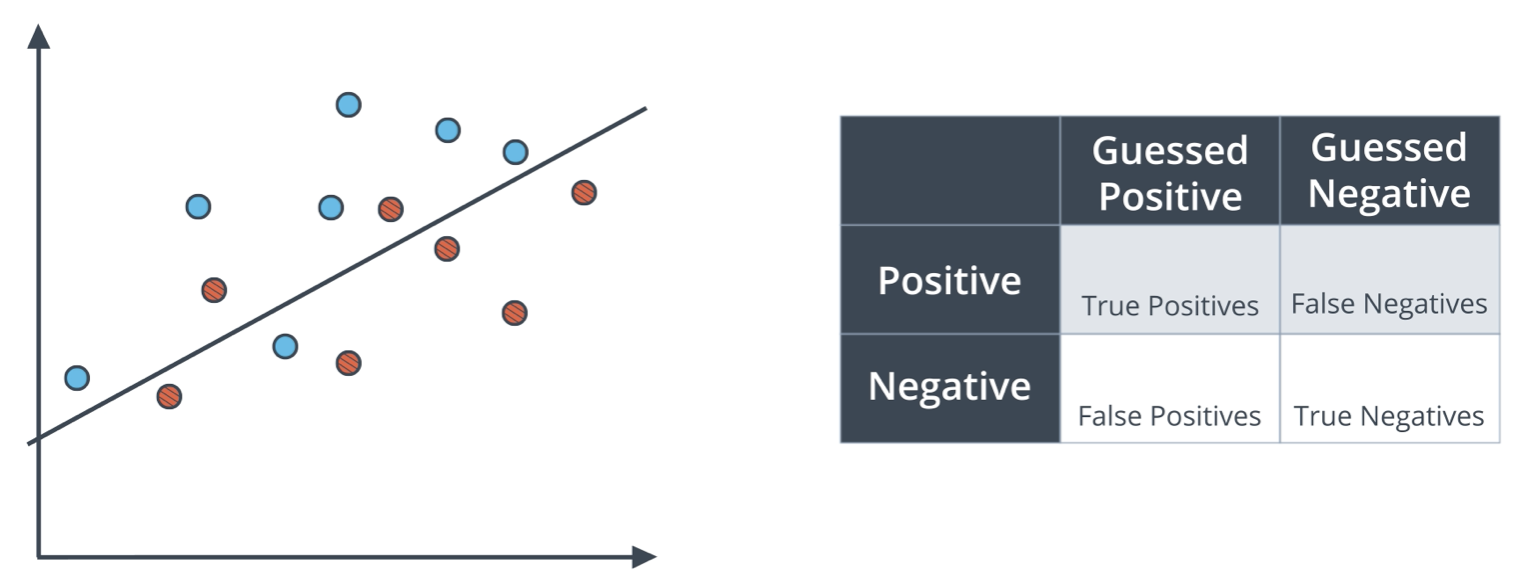
- True Positives: 6 blue points above line.
- True Negatives: 5 red points below line.
- False Positives: 2 red points above line.
- False Negatives: 1 blue point below line.
The labels above are the most common, but in the literature there are other names:
- False Positive: Type 1 Error or Error of the first kind - In the medical example, this is when a healthy patient is diagnosed sick.
- False Negative: Type 2 Error or Error of the second kind - In the medical example, this is when a sick patient is diagnosed healthy.
Accuracy
Accuracy is one of the ways to measure how good a model is. In the context of the medical example introduced earlier, the accuracy answers the following question. Out of all the patients, how many did we classify correctly?

$$Accuracy = \frac{1000+8000}{10000} = 90\%$$
from sklearn.metics import accuracy_score
accuracy_score(y_true, y_pred)
If we are given an array of predicted values and actual values, accuracy can also be predicted manually with the following.
def accuracy(actual, preds):
return np.sum(preds == actual)/len(actual)
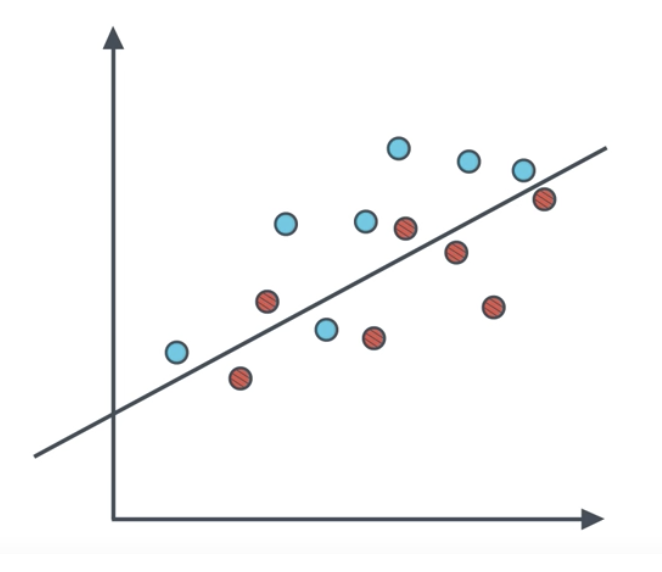
In the example below, the accuracy is $\frac{6+5}{14} = \frac{11}{14} = 78.57\%$.
Accuracy is not always the best metric to use to determine a model’s performance. Specifically, if a dataset is skewed significantly toward one or the other of two binary labels, the model may have very high accuracy simply by choosing one of those two. Consider an example dataset of credit card transactions that has 284,335 valid transactions and 472 fraudulent transactions.

By classifying all of the transactions as valid, the model has an accuracy of
$$Accuracy = \frac{284335}{284335 + 472}=99.83\%$$
But, this is clearly not a good model since it does not catch any of the fraudulent transactions. So, other metrics are needed.
False Negatives and Positives
As discussed briefly above, the type of model under consideration dictates how the model should balance the ratio of False Negatives to False Positives.
In a medical model, it is worse for a sick patient to be diagnosed as healthy: a False Negative. A False Positive implies sending a healthy person to get more tests. This is inconvenient, but ok. A False Negative implies sending a sick person home, which could be deadly.
In a spam email model, it is worse for a legitimate email to be classified as spam: a False Positive. A False Negative implies a spam message will make its way into your inbox. This is inconvenient, but ok. A False Positive implies possibly missing a very important email, which could be costly.

Next, I define precision and recall, which are the metrics that would be needed to optimize the models described above.

Precision
Precision is defined as the proportion of data that was predicted positive to the data was actually positive.
Precision focuses on the predicted positive values in the dataset. By optimizing based on precision values, you are determining if you are doing a good job of predicting the positive values, as compared to predicting negative values as positive.
$$Precision=\frac{True\ Positives}{True\ Positives+False\ Positives}$$
from sklearn.metics import precision_score
precision_score(y_true, y_pred)
If we are given an array of predicted values and actual values, precision can also be calculated manually with the following.
def precision(actual, preds):
return np.sum(np.logical_and((preds == 1), (actual == 1))) / (np.sum(preds == 1))
In the case of the medical model, precision answers the following question. Out of all the patients we diagnosed as sick, what proportion were actually sick?
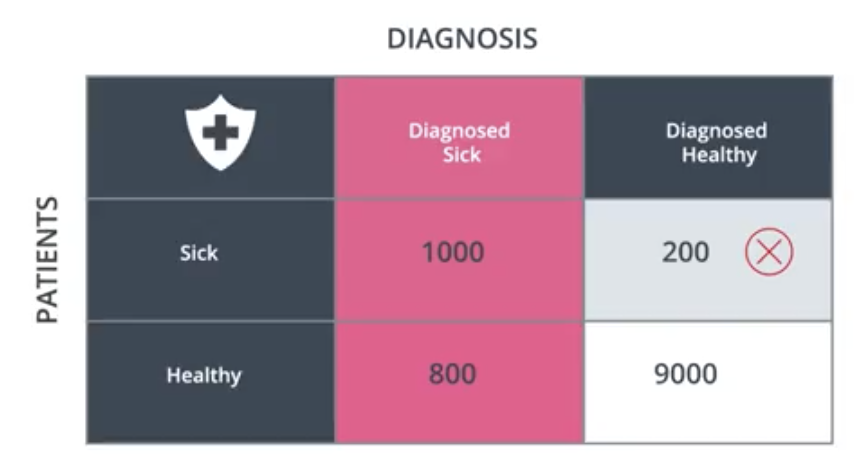
$$Precision=\frac{1000}{1000+800}=55.6\%$$
For the spam email model, the question is the following. Out of all emails classified as spam, how many were spam?
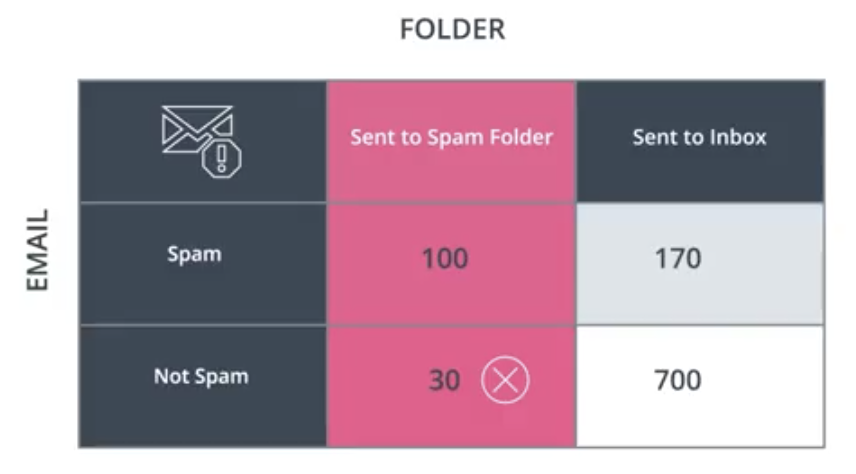
$$Precision=\frac{100}{100+30}=76.9\%$$
The precision of the following model is the proportion of points predicted positive that actually are positive. Remember the points above the line are predicted positive, and the points that are blue actually are positive.
$$Precision=\frac{6}{6+2}=75\%$$
Recall
Recall is defined as the proportion of data that was actually positive to the data that was predicted positive.
Recall focuses on the actual positive values in the dataset. By optimizing based on recall values, you are determining if you are doing a good job of predicting the positive values without regard of how you are doing on the actual negative values.
$$Recall=\frac{True\ Positives}{True\ Positives+False\ Negatives}$$
from sklearn.metics import recall_score
recall_score(y_true, y_pred)
If we are given an array of predicted values and actual values, recall can also be calculated manually with the following.
def recall(actual, preds):
return np.sum(np.logical_and((preds == 1), (actual == 1))) / (np.sum(actual == 1))
In the case of the medical mode, recall answers the following question. Out of all the patients that were sick, what proportion were diagnosed sick?
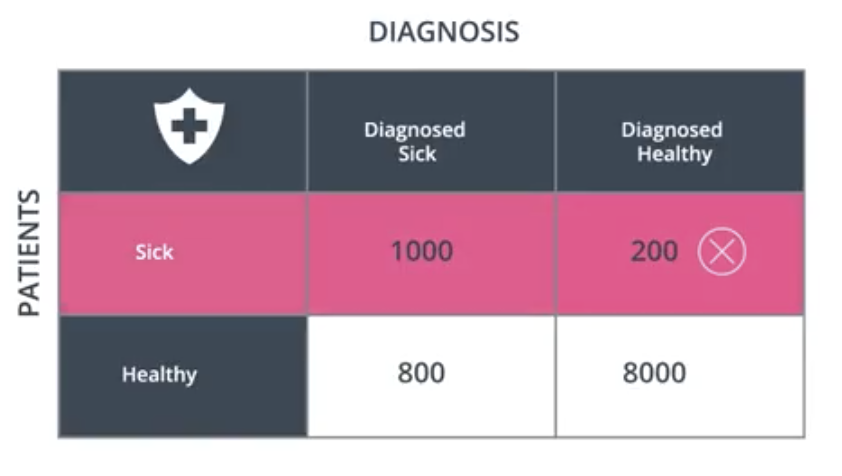
$$Recall=\frac{1000}{1000+200}=83.3\%$$
In the case of the spam email model, the question is the following. Out of all the emails that were spam, what proportion were classified as spam?
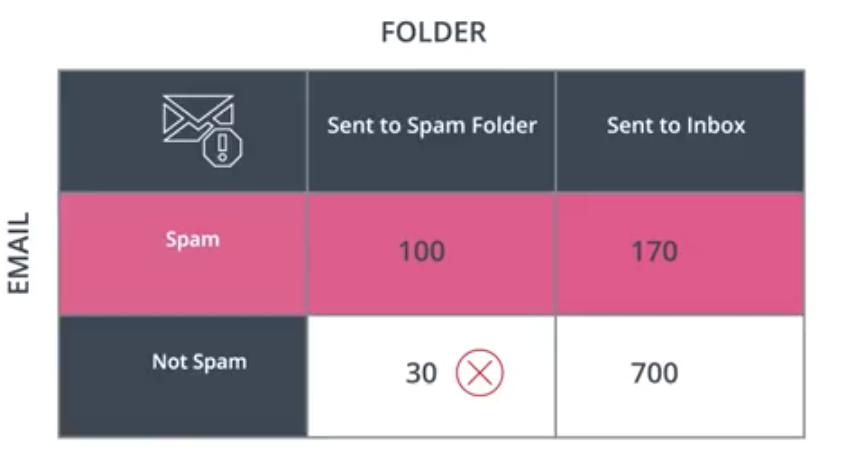
$$Recall=\frac{100}{100+170}=37.0\%$$
The recall of the following model is the proportion of points that actually were positive that were predicted positive. Remember the points above the line are predicted positive, and the points that are blue actually are positive.

$$Recall=\frac{6}{7}=85.7\%$$
F1 Score
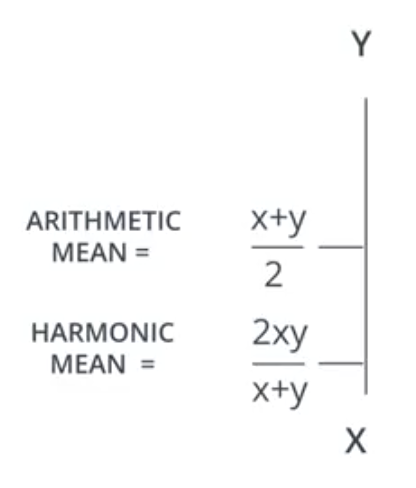
The F1 Score, or $F_1\ Score$, is a means of combining both the precision and recall into a single metric for simplicity. The F1 Score for a model is the harmonic mean of the model’s precision and recall. The harmonic mean is a different calculation than the arithmetic mean, and is always lower.
$$Harmonic\ Mean = \frac{2xy}{x+y}$$
from sklearn.metics import f1_score
f1_score(y_true, y_pred)
If we are given an array of predicted values and actual values, the f1 score can also be calculated manually with the following in combination with the functions defined above.
def f1(actual, preds):
numerator = 2 * precision(actual, preds) * recall(actual, preds)
denominator = precision(actual, preds) + recall(actual, preds)
return numerator / denominator
By way of illustration, consider the following sets of values. Note that it is lower than the arithmetic mean in all cases. This property of the harmonic mean makes it a better measure of the performance of a model in extreme situations where the precision is significantly lower than the recall, or vice versa.
| Precision | Recall | Average | Harmonic Mean |
|---|---|---|---|
| 1 | 0 | 0.5 | 0 |
| 0.2 | 0.8 | 0.5 | 0.32 |
| 0.556 | 0.833 | 0.695 | 0.667 |
By way of further example, revisit the credit card fraud example from before. Remember that the model is that all 284,807 transactions are legitimate.
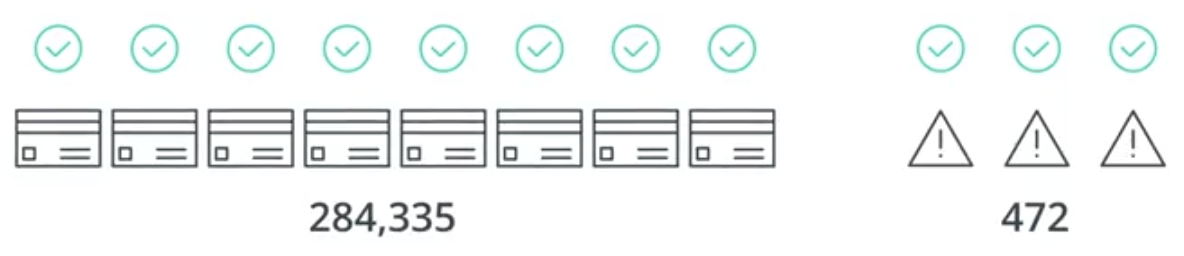
In that situation, $Accuracy=99.83\%$ and $Precision=100\%$, but the $Recall = 0\%$ and the $F_1\ Score = 0$.
Fundamentally, what the F1 Score does is combine the precision and recall values into a single metric using a rough average, while also raising a flag (in the form of a lower score) when one is significantly lower than the other.
$F_{\beta}\ Score$
The $F_{\beta}\ Score$ is a more general form of the $F_1\ Score$ that enables us to change the relative importance of precision and recall in our calculations. As shown in the image below, the $F_1\ Score$ values precision and recall equally.

from sklearn.metrics import fbeta_score
fbeta_score(y_true, y_pred, beta=1)
The mathematical formula for $F_{Beta}$ is shown below.
$$F_{\beta}\ Score = \frac{(1+\beta^2) \times Precision \times Recall}{\beta^2 \times Precision + Recall}$$
If a model needs to value precision more than recall, as in the spam email model, then a value of $\beta$ less than 1 should be used. Conversely, if recall is a higher priority, then a value of $\beta$ higher than 1 should be used.
In the formula set forth above:
- If $\beta=0$, we get precision.
- If $\beta=\infty$, we get recall.
Consider models for:
- Detecting malfunctioning parts on the space station: we can’t afford any malfunctioning parts, and its okay if we overcheck some parts.
- This is a high recall model and should have a relatively large beta. $\beta=2$.
- Sending phone notifications about videos a user might like: since sending notifications are free, we won’t get harmed if we send them to more people than we need to. But, we could annoy users, and we prefer finding interested users.
- This model has a need for balance in precision and recall. $\beta=1$.
- Sending promotional material in the mail to potential clients: since sending promotional material costs money, we don’t want to send it to people who wouldn’t be interested.
- This is a high precision model and should have a relatively small beta. $\beta=0.5$
Note that setting values for $\beta$ is not an exact science. It requires data intuition and a lot of experimentation.
ROC Curve (Receiver Operating Characteristic)
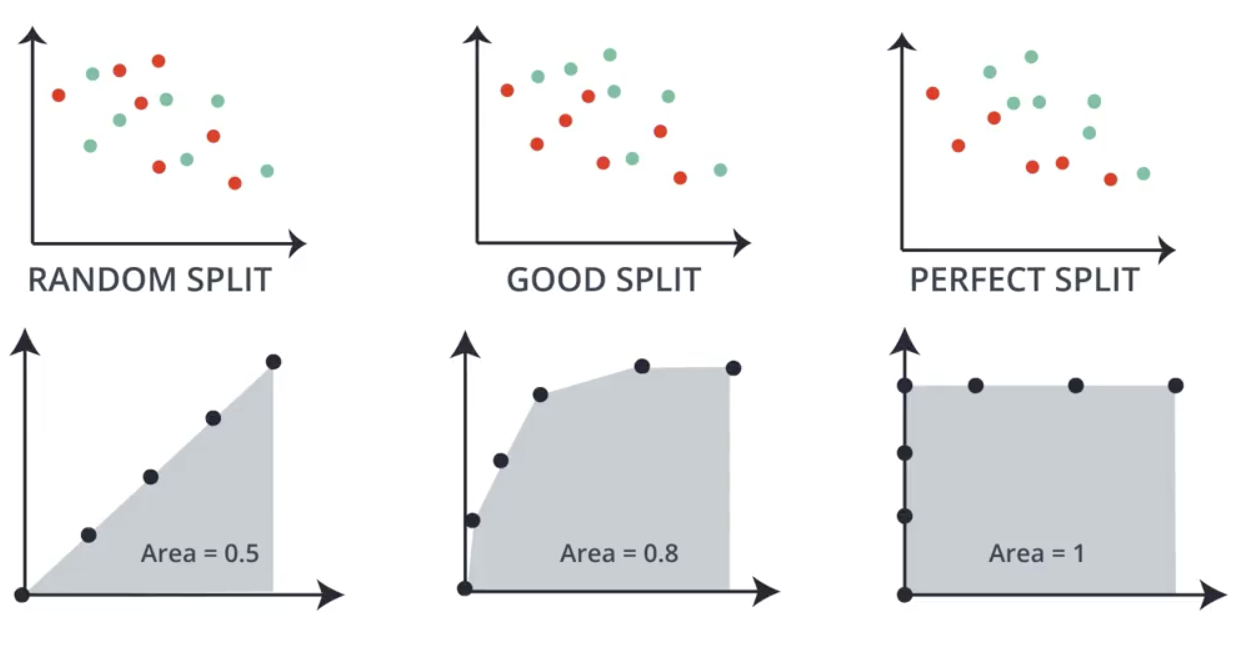
The ROC Curve is another way to classify models. It provides an indication of how well the model splits the data.
Consider the following one-dimensional sets of data. Intuitively, the splits shown can be considered as perfect, good, or random (bad) splits. The ROC Curve provides a number between 0 and 1, like those shown below, depending on the quality of the split, helping us to quantify and formalize the quality classifications we arrived at intuitively.
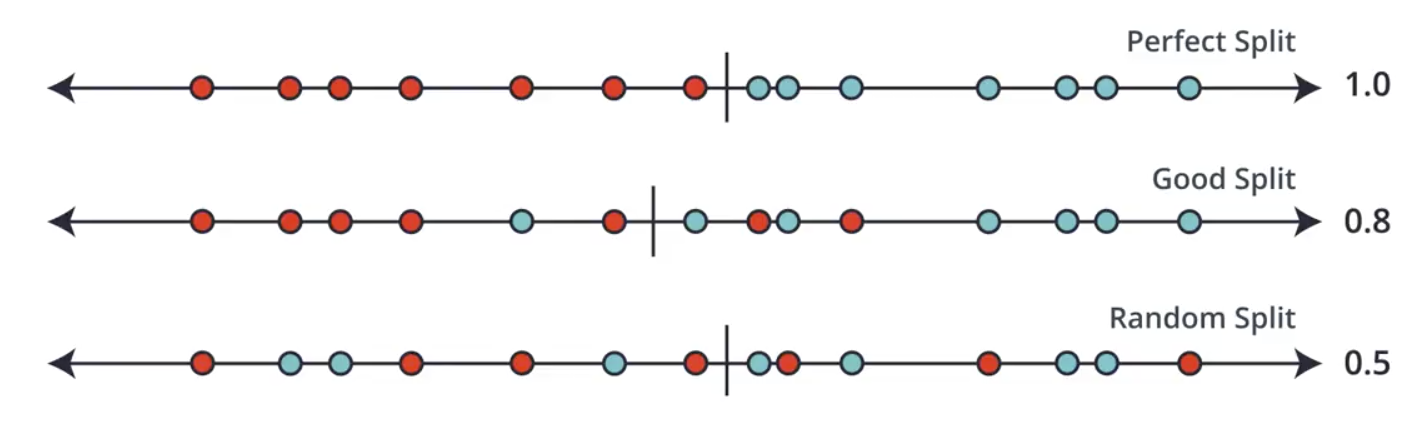
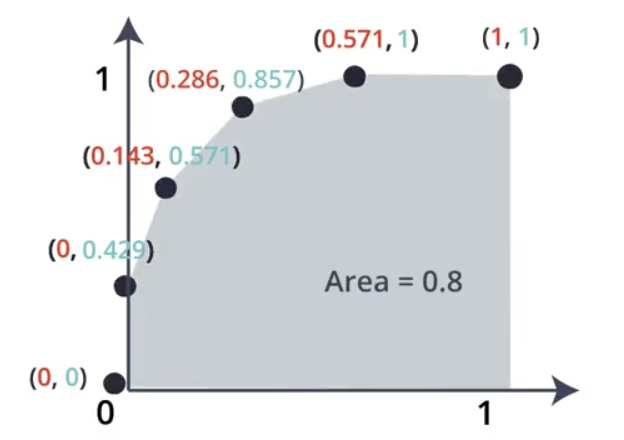
To construct these values, we first create the ROC Curve. Building the curve requires determining the True Positive Rate and False Positive Rate for all of the possible boundaries in the dataset. An example of a single split is shown below.


$$True\ Positive\ Rate=\frac{6}{7}=0.857$$

$$False\ Positive\ Rate=\frac{2}{7}=0.286$$
These two values form the coordinates for a single point on the ROC curve.

Repeating the process for the remaining possible splits on the dataset builds a set of points, which are then plotted. Calculating the area under the resulting curve results in the numeric classification we are looking for.

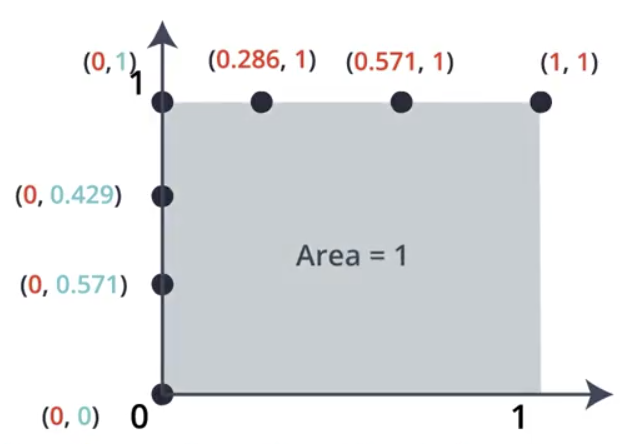
The area under the ROC curve is always 1 for a perfect split.

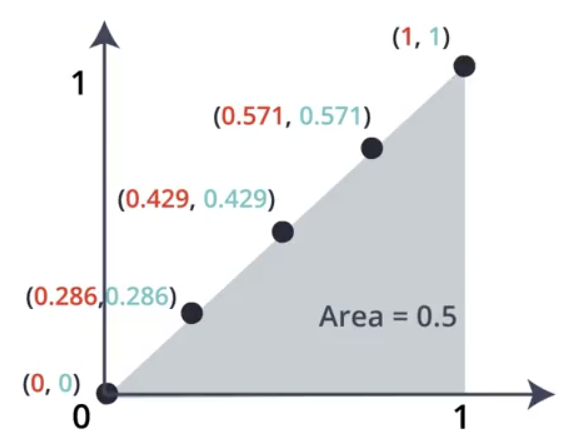
For a random split where the data is not split well, the area under the ROC curve is usually around 0.5.

The area under the ROC Curve can be less than 0.5, but this means that the model is classifying more than half of the points incorrectly. Flipping the data may help in this scenario.