Classifying Fashion MNIST
This example uses the Fashion-MNIST dataset, a drop-in replacement for the MNIST dataset. MNIST is actually quite trivial with neural networks. Its possible to easily achieve better than 97% accuracy. Fashion-MNIST is a set of 28x28 greyscale images of clothes. It’s more complex than MNIST, so it’s a better representation of the actual performance of your network, and a better representation of datasets used in the real world.
First, load the dataset through torchvision.
import torch
from torchvision import datasets, transforms
# Define a transform to normalize the data
transform = transforms.Compose([transforms.ToTensor(),
transforms.Normalize((0.5,), (0.5,))])
# Download and load the training data
trainset = datasets.FashionMNIST('~/.pytorch/F_MNIST_data/',
download=True,
train=True,
transform=transform)
trainloader = torch.utils.data.DataLoader(trainset,
batch_size=64,
shuffle=True)
# Download and load the test data
testset = datasets.FashionMNIST('~/.pytorch/F_MNIST_data/',
download=True,
train=False,
transform=transform)
testloader = torch.utils.data.DataLoader(testset,
batch_size=64,
shuffle=True)
The following is a helper function to print one of the images.
import matplotlib.pyplot as plt
import numpy as np
def imshow(image, ax=None, title=None, normalize=True):
if ax is None:
fig, ax = plt.subplots()
image = image.numpy().transpose((1, 2, 0))
if normalize:
mean = np.array([0.485, 0.456, 0.406])
std = np.array([0.229, 0.224, 0.225])
image = std * image + mean
image = np.clip(image, 0, 1)
ax.imshow(image)
ax.spines['top'].set_visible(False)
ax.spines['right'].set_visible(False)
ax.spines['left'].set_visible(False)
ax.spines['bottom'].set_visible(False)
ax.tick_params(axis='both', length=0)
ax.set_xticklabels('')
ax.set_yticklabels('')
return ax
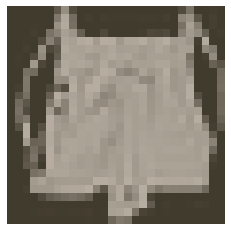
Here we can see one of the images.
image, label = next(iter(trainloader))
imshow(image[0,:]);
Defining the Network Architecture
Defining the network architecture, IE, “build the network.”
As with MNIST, each image is 28x28 which is a total of 784 pixels, and there are 10 classes. Notes regarding recommended network architecture for fashion-mnist:
- At least one hidden layer is necessary.
- ReLU activations are recommended for the layers
- Logits or log-softmax are recommended from the forward pass.
For straightforward comparison with results on the standard MNIST, use the same network setup.
from torch import nn
model = nn.Sequential(nn.Linear(784, 128),
nn.ReLU(),
nn.Linear(128, 64),
nn.ReLU(),
nn.Linear(64, 10),
nn.LogSoftmax(dim=1))
Train the network
Now, create the network and train it.
First, define:
- the criterion (something like
nn.CrossEntropyLoss) and - the optimizer (typically
optim.SGDoroptim.Adam).
from torch import optim
criterion = nn.NLLLoss()
optimizer = optim.SGD(model.parameters(),
lr=0.003)
Then, train the network. The training pass is a fairly straightforward process:
- Make a forward pass through the network to get the logits
- Use the logits to calculate the loss
- Perform a backward pass through the network with
loss.backward()to calculate the gradients - Take a step with the optimizer to update the weights
A training loss rate below 0.4 should be possible on the dataset.
epoch = 1
while True:
running_loss = 0
for images, labels in trainloader:
# Flatten MNIST images into a 784 long vector
images = images.view(images.shape[0], -1)
optimizer.zero_grad()
output = model(images)
loss = criterion(output, labels)
loss.backward()
optimizer.step()
running_loss += loss.item()
training_loss = running_loss/len(trainloader)
print("Epoch, Loss: {:2}, {:1.3}".format(epoch, training_loss))
epoch += 1
if training_loss < 0.4:
break
Epoch, Loss: 1, 1.65
Epoch, Loss: 2, 0.834
Epoch, Loss: 3, 0.665
Epoch, Loss: 4, 0.6
Epoch, Loss: 5, 0.559
Epoch, Loss: 6, 0.531
Epoch, Loss: 7, 0.509
Epoch, Loss: 8, 0.492
Epoch, Loss: 9, 0.479
Epoch, Loss: 10, 0.467
Epoch, Loss: 11, 0.457
Epoch, Loss: 12, 0.449
Epoch, Loss: 13, 0.441
Epoch, Loss: 14, 0.434
Epoch, Loss: 15, 0.428
Epoch, Loss: 16, 0.422
Epoch, Loss: 17, 0.417
Epoch, Loss: 18, 0.412
Epoch, Loss: 19, 0.407
Epoch, Loss: 20, 0.403
Epoch, Loss: 21, 0.398
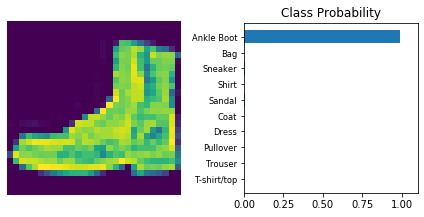
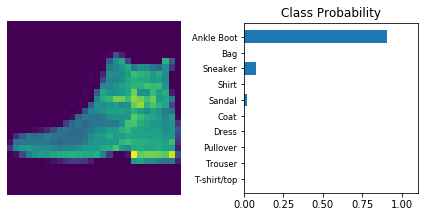
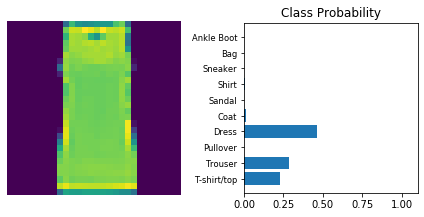
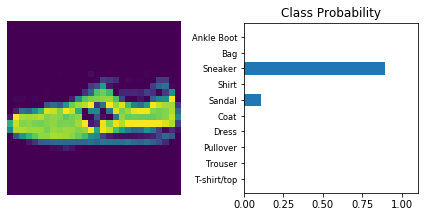
The following is a helper function to print
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
def view_classify(img, ps):
ps = ps.data.numpy().squeeze()
fig, (ax1, ax2) = plt.subplots(figsize=(6,9), ncols=2)
ax1.imshow(img.resize_(1, 28, 28).numpy().squeeze())
ax1.axis('off')
ax2.barh(np.arange(10), ps)
ax2.set_aspect(0.1)
ax2.set_yticks(np.arange(10))
ax2.set_yticklabels(['T-shirt/top',
'Trouser',
'Pullover',
'Dress',
'Coat',
'Sandal',
'Shirt',
'Sneaker',
'Bag',
'Ankle Boot'], size='small');
ax2.set_title('Class Probability')
ax2.set_xlim(0, 1.1)
plt.tight_layout()
dataiter = iter(testloader)
for _ in range(10):
images, labels = dataiter.next()
img = images[0]
# Convert 2D image to 1D vector
img = img.resize_(1, 784)
# Turn off gradients to speed up this part
with torch.no_grad():
logps = model(img)
# Output of the network are log-probabilities, need to take exponential for probabilities
ps = torch.exp(logps)
# Plot the image and probabilities
view_classify(img.resize_(1, 28, 28), ps)
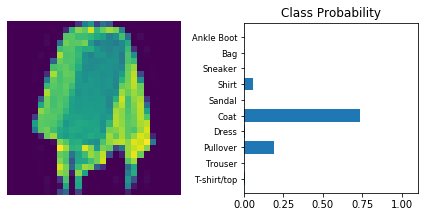
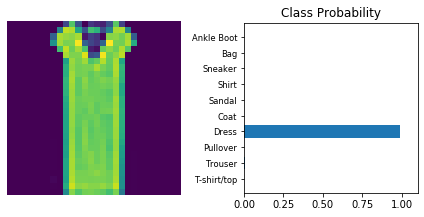
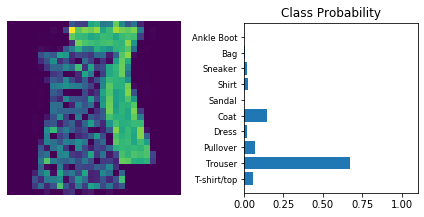

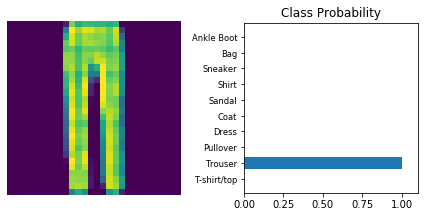
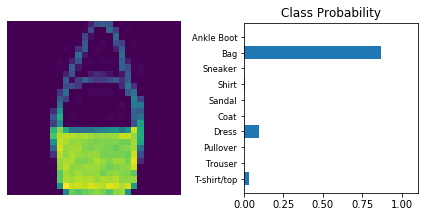
Copyright © 2018 Udacity