Normalization

• Mapping of EER Diagrams to Relations will always result in a Normalized database.
• Normalized databases are laid out in such a manner that it is easy to enforce functional dependencies.
  • How do we normalize the relations without information loss and so that the functional dependencies can be enforced?

Normalization Rules

1. No redundancy of facts
2. No cluttering of facts
3. Must preserve information
4. Must preserve functional dependencies

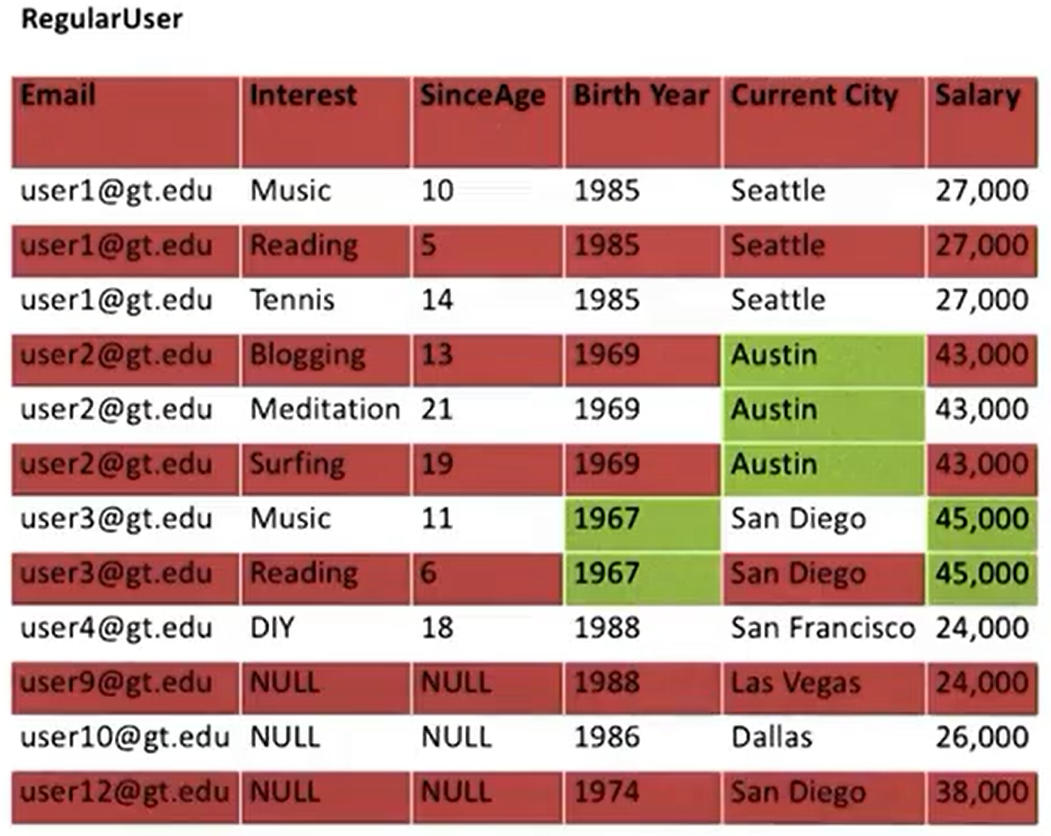
Problems with Relations

NOT a relation – NF2 (“Non-first normal form” data structure)

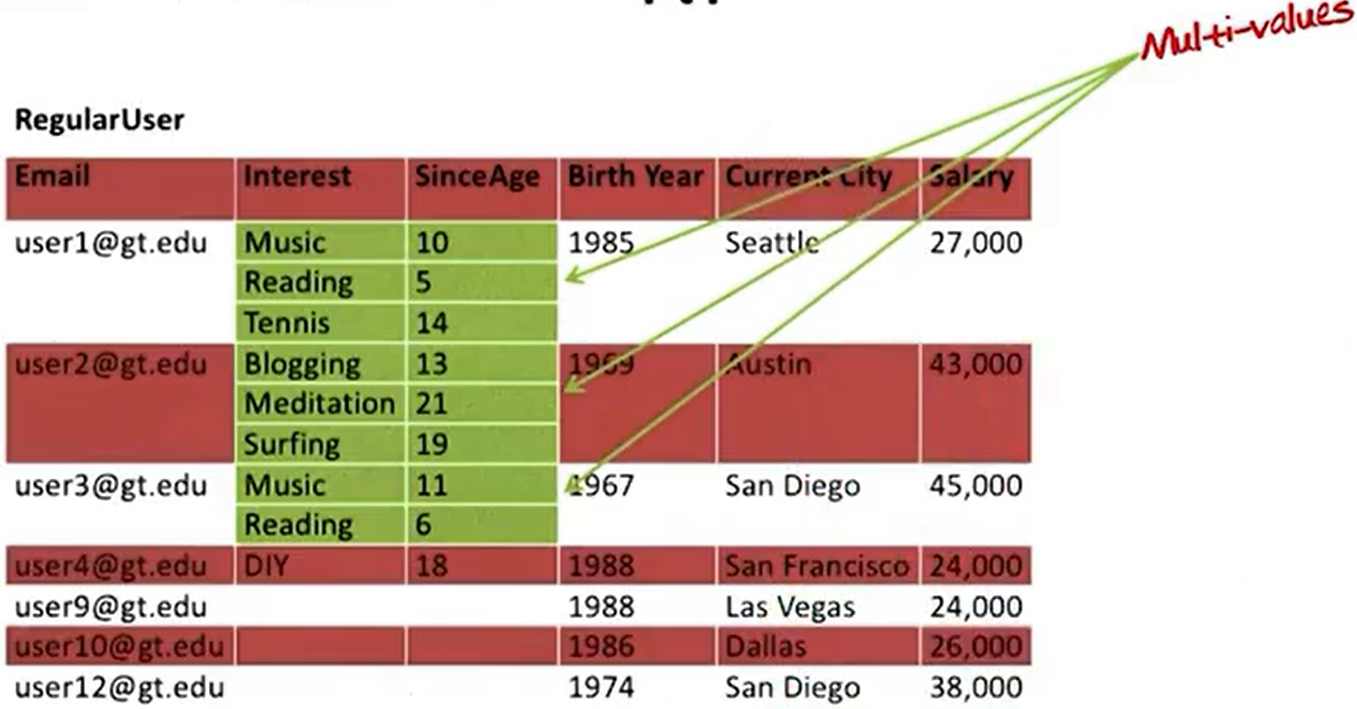
Redundancy

• Changing one of the redundant cells to a different value would result in an ambiguous relation

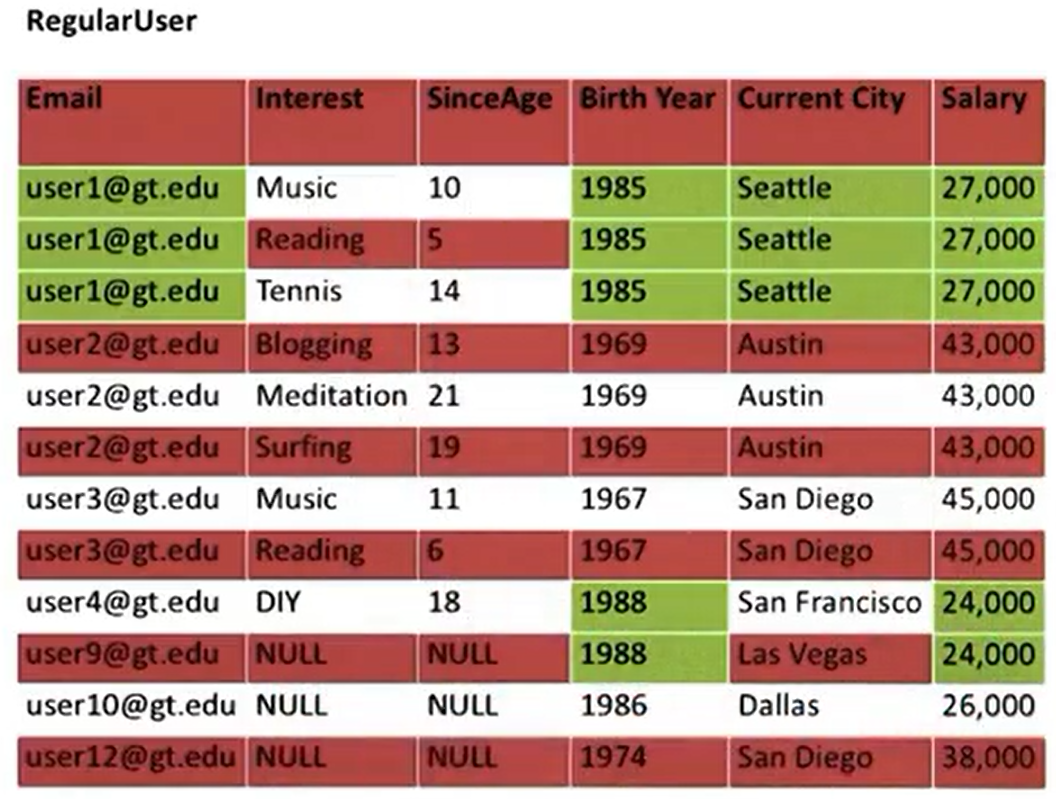
Insertion Anomaly

• Inserting incomplete rows.

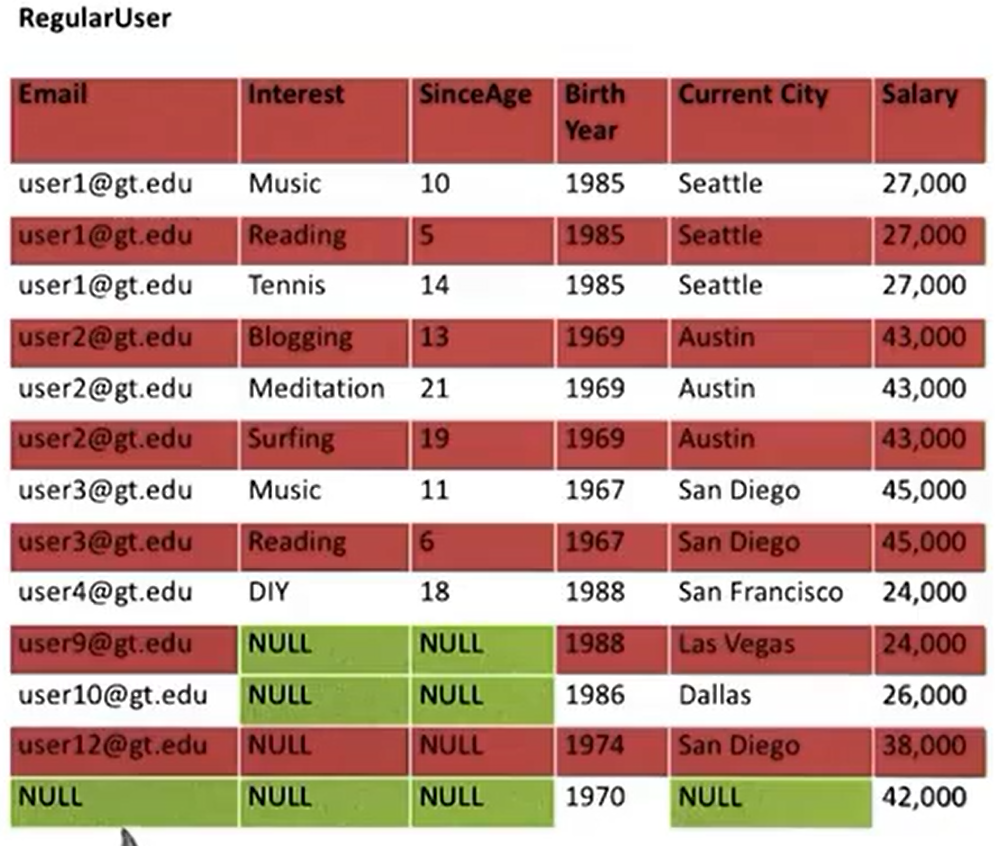
Deletion Anomaly

• Deleting rows necessarily deletes information.

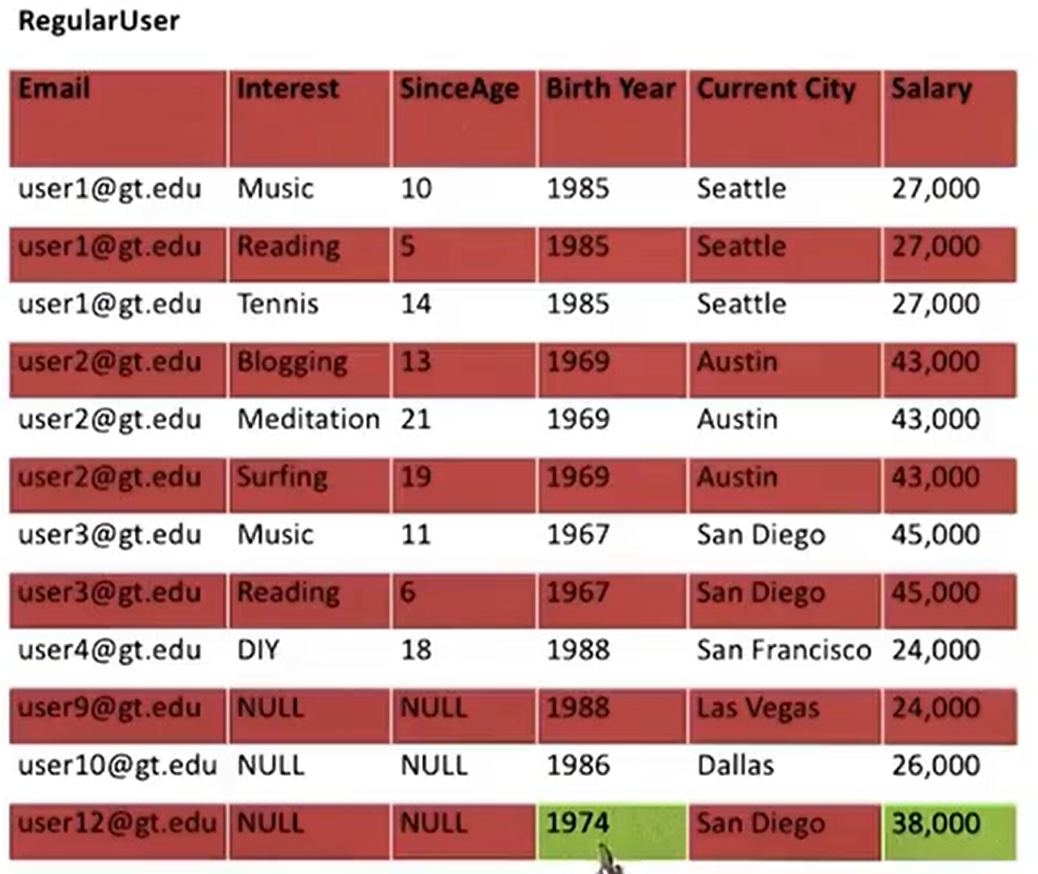
Update Anomaly

• Updates may need to be made in multiple places.

Information Loss

• If a relation is decomposed into two other relations, recombining them together may result in too many rows. This additional information is fictitious, so it is information “loss” because the new, fake information “waters down” the existing true information.

Dependency Loss

• If a relation is decomposed into two other relations, then we cannot enforce the functional dependencies that are split between the two relations.
  • If two attributes do not end up in the same table, then the relationship between them cannot be enforced.

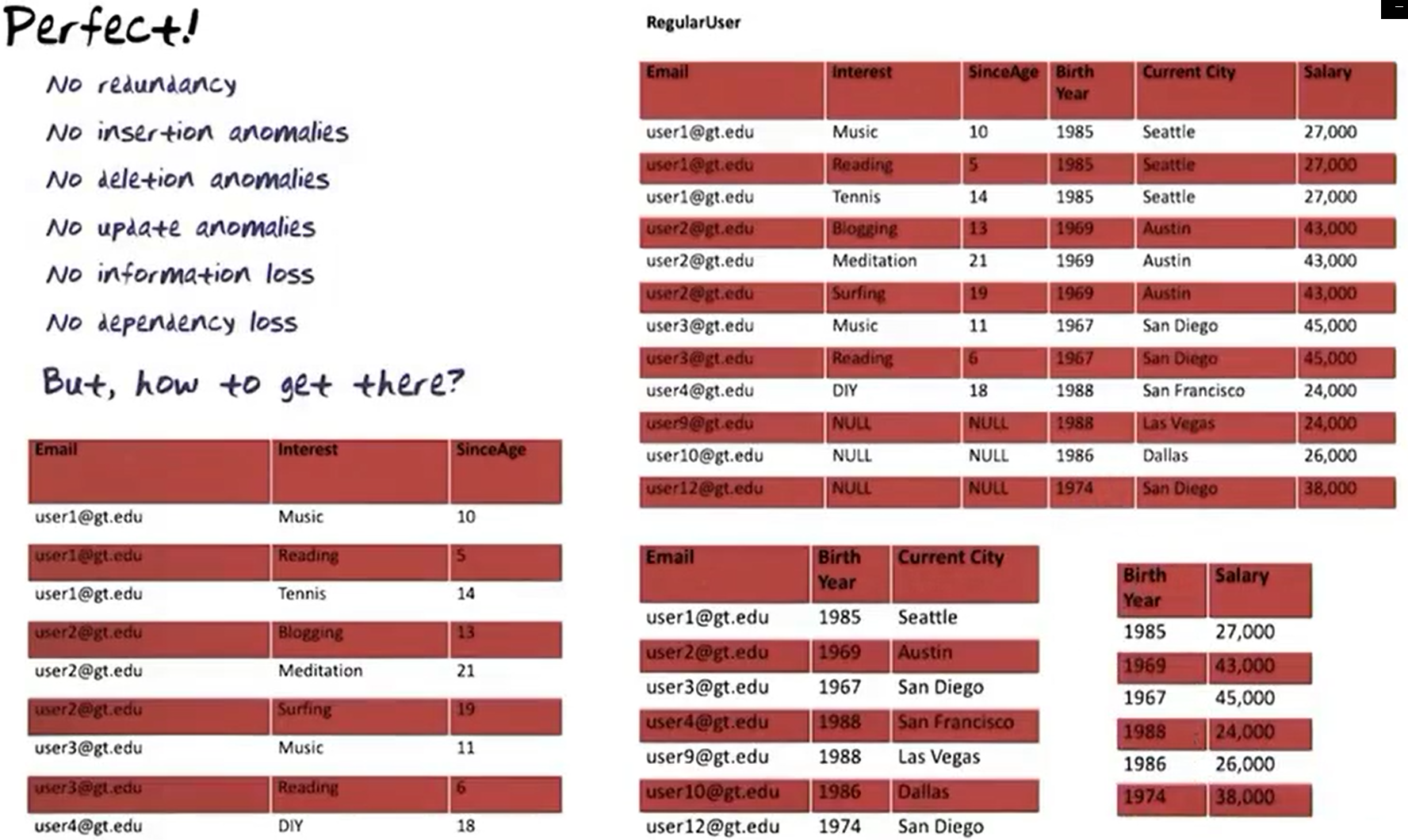
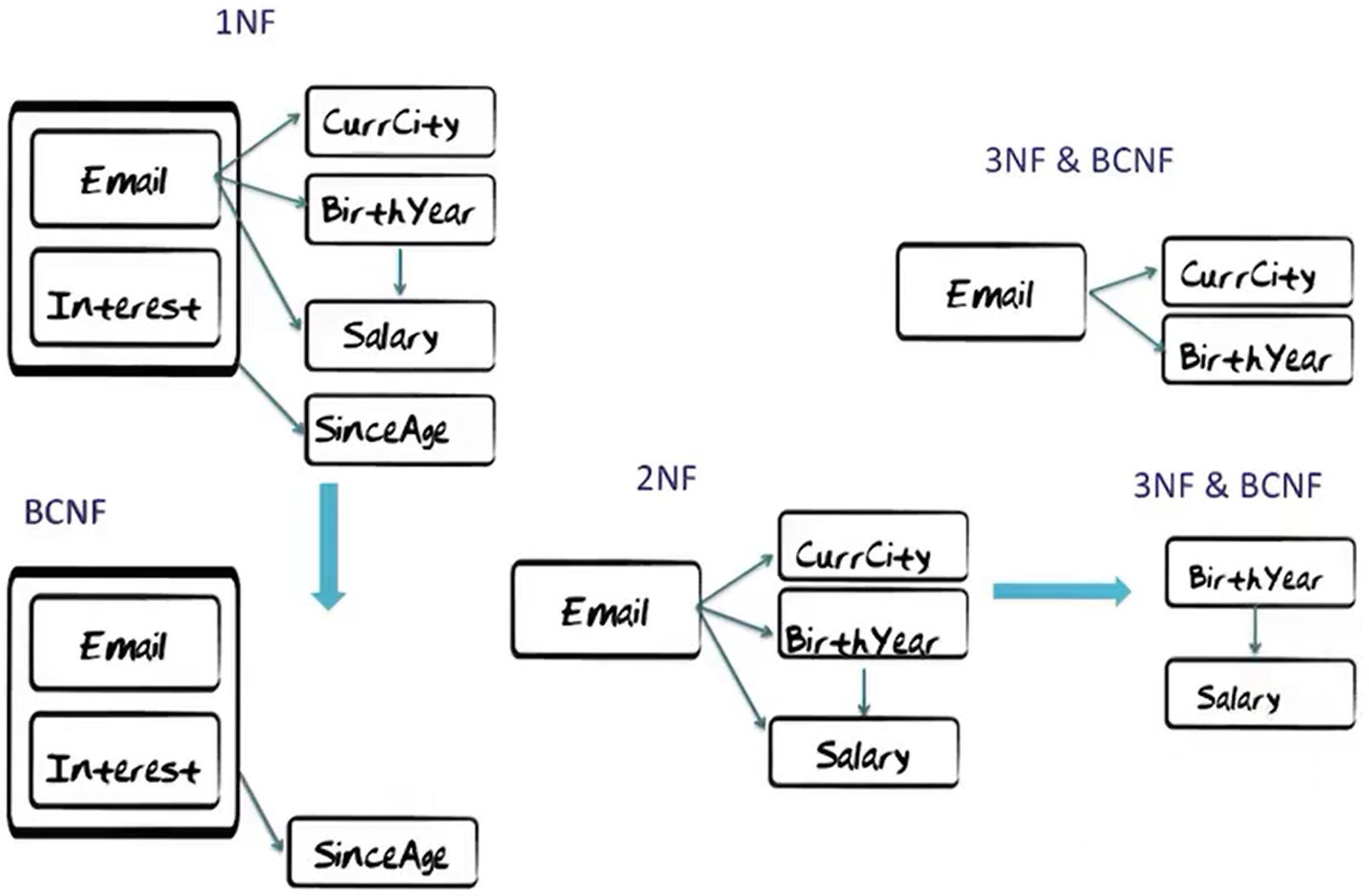
Perfect Decomposition

• Bottom three tables are a perfect decomposition of the top table.
  • The functional dependencies have all been captured in relations.

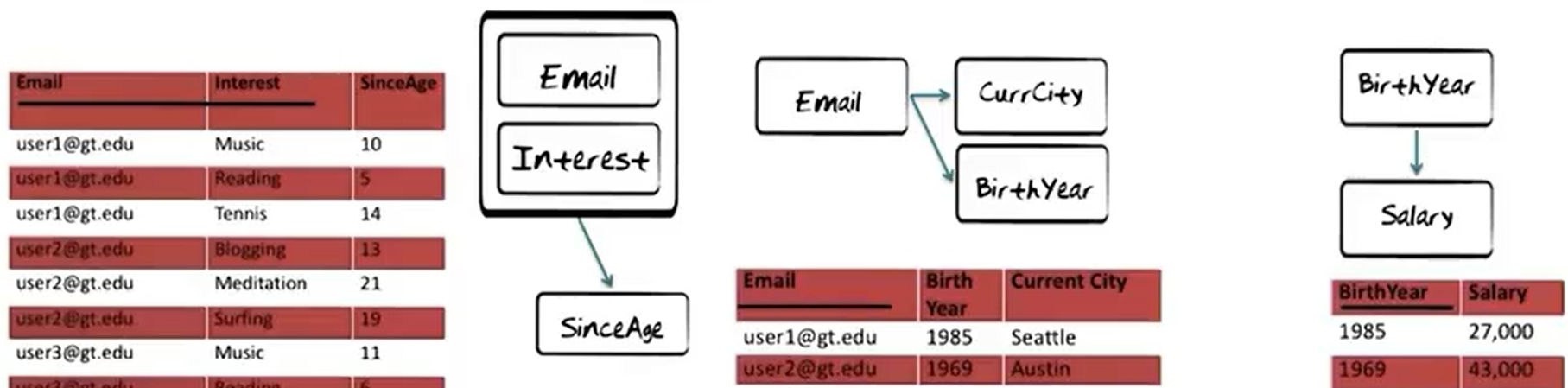
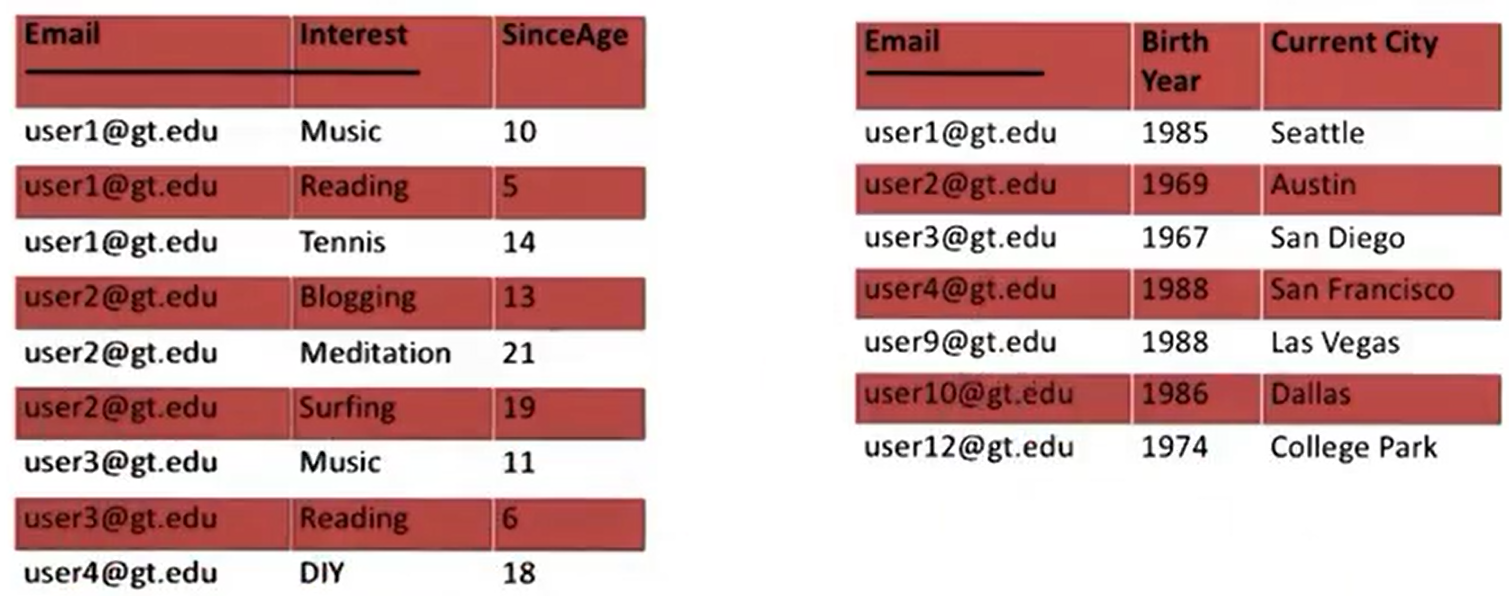
Functional Dependencies

• Y is functionally dependent on X in R if and only if for each X in a relation there is precisely one Y in that relation.
  • In table above, CurrentCity is functionally dependent upon Email
  • SinceAge is functionally dependent upon Email and Interest

Full Functional Dependencies

• Y is fully functionally dependent on X if and only if Y is functionally dependent on X and Y is not functionally dependent on any proper subset of X.
  • In table above, SinceAge in table above is fully functionally dependent upon Email and Interest
  • CurrentCity is not fully functionally dependent upon Email and Interest because it is dependent upon Email alone.

Functional Dependencies and Keys

• We use keys to enforce full functional dependencies X -> Y (“X determines Y”)
  • Attribute Closure: Attribute closure of an attribute set can be defined as set of attributes which can be functionally determined from it.
    • This includes those attributes themselves, due to reflexive rule.
• In a relation, the values of the key are unique, so it enforces a function
• Underlined attributes are the key.

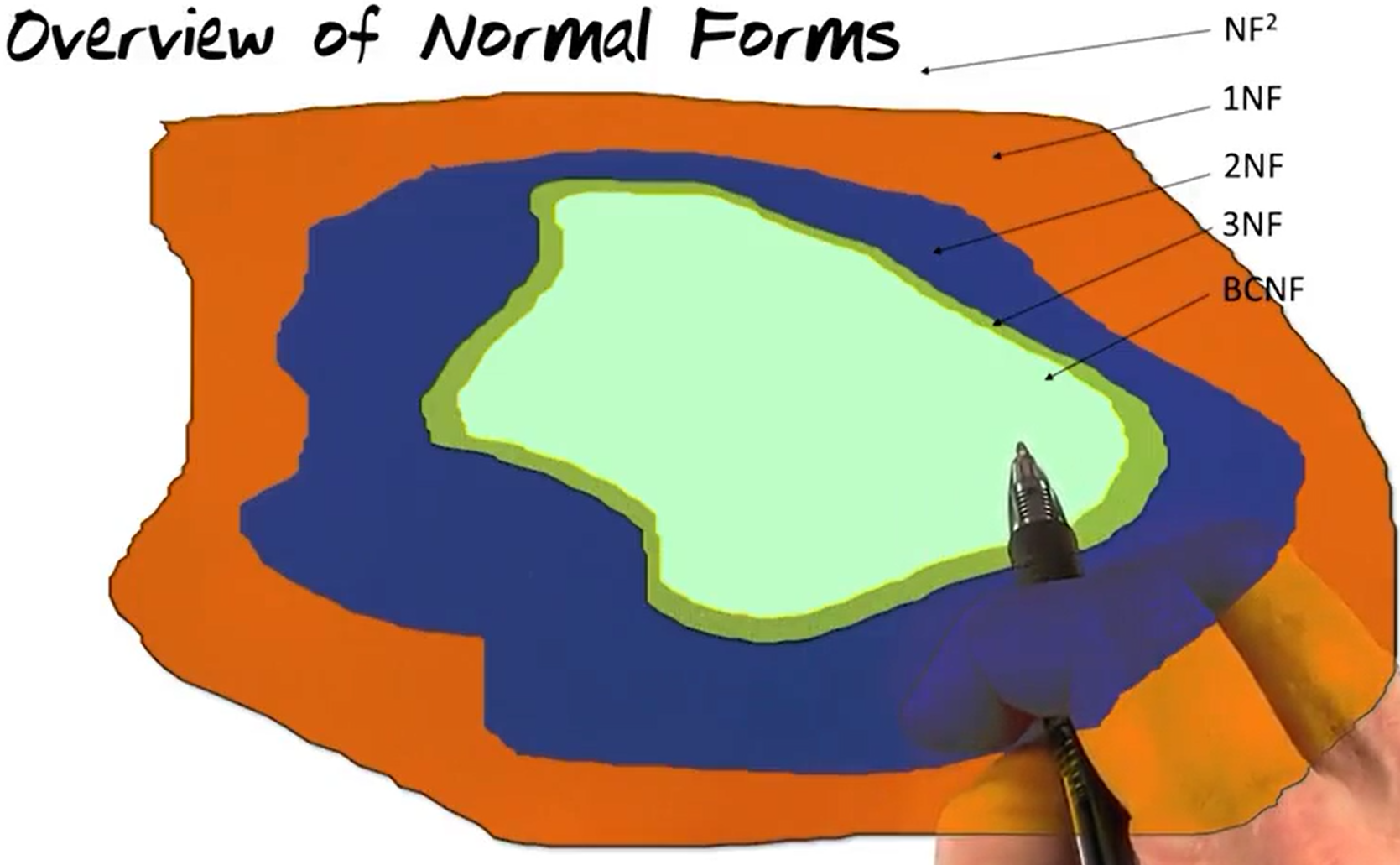
Overview of Normal Forms

The forms shown below are subsets of the preceding.

• NF2 – “Non-first normal forms,” or, the whole set of data structures. Many of these are not relations.
• 1NF – “First-Normal Form relations,” a subset of NF2
• 2NF – “Second-Normal Form relations,” a subset of 1NF
• 3NF – “Third-Normal Form relations,” a subset of 2NF
• BCNF – “Boyce-Codd Normal Form,” a subset of 3NF

Note: In practice, most of the time, when normalizing from 2NF to 3NF, you generally end up with something that is also BCNF.

Normal Form Definitions

• NF2: “Non-first normal forms,” or, the whole set of data structures. Many of these are not relations.
• 1NF: a relation R is in 1NF iff (if and only if) all domain values are atomic. Note that we have defined relations as a data structure where the domain values are pulled from sets of atomic values. So, all relations are automatically born in 1NF.
• 2NF: a relation R is in 2NF iff R is in 1NF and every non-key attribute is fully dependent on the key.
• 3NF: a relation R is in 3NF iff R is in 2NF and every non-key attribute is non-transitively dependent on the key.
• BCNF: The desirable form. A relation R is in BCNF iff every determinant is a candidate key.
  • Determinant: a set of attributes on which some other attribute is fully functionally dependent.
  • Candidate Key: a combination of attributes that can be uniquely used to identify a database record without referring to any other data. Each table may have one or more candidate. One of these candidate keys is selected as the table primary key.

“All attributes must depend on the key (1NF), the whole key (2NF), and nothing but the key (3NF), so help me Codd!” – Kent, 83; Diehr, 89

Ted Codd is the inventor of relational databases.

See following example of “relation decomposition”

Armstrong’s Rules

• Reflexivity: if Y is part of X, thend X -> Y (where -> is the same as “determines”) Email, Interest -> Interest
• Augmentation: if X -> Y, then WX -> WY If Email -> BirthYear, then Email, Interest -> BirthYear, Interest
• Transitivity: if X -> Y and Y -> Z, then X -> Z Email -> BirthYear and BirthYear -> Salary, then Email -> Salary

Two questions to ask when decomposing relations:

How to guarantee lossless joins?

• The join field must be a key in at least one of the relations
  • If this is the case, then there will not be duplication when combining the tables together

How to guarantee preservation of Functional Dependencies?

• The meaning implied by the remaining functional dependencies must be the same! 3NF and BCNF
• The set of BCNF relations is a proper subset of 3NF relations
• There does exist relations which can only be decomposed to 3NF, but not to BCNF, while being lossless and dependency preserving.
• It can only happen when the relation has overlapping keys.
• When normalizing, follow the steps above, and the transition from a 2NF relation to a 3NF relation will almost always result in a relation that is also BCNF.

Other Notes

• Normalize a relation in order to reduce redundancy.
• Repeated use of inference (Armstrong?) rules on a superkey will generate all the attributes of the relation.
• Functional dependency relationships that “form a circle” of linked attributes can be decomposed into a set of BCNF relations without information or dependency loss.
• Meaning of a single functional dependency includes the following:
  • Any combination of the input attributes implies a unique value of the output
  • If one tuple has the same values of the input tuples as another tuple, then that tuple must have the same value of the output tuple
• Desirable properties of a relational decomposition include:
  • Dependency preservation
  • Non-additive (lossless) joins
  • Attribute preservation