Using PCA on Cars Dataset
import pandas as pd
import numpy as np
from sklearn.decomposition import PCA
from sklearn.preprocessing import StandardScaler
import matplotlib.pyplot as plt
The dataset for this example consists of 387 cars with 18 features. 7 of these features are dummy variables.
c = pd.read_csv('pca-on-cars-dataset/cars.csv')
c.info()
c.head().T
<class 'pandas.core.frame.DataFrame'>
Index: 387 entries, Acura 3.5 RL to Volvo XC90 T6
Data columns (total 18 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 Sports 387 non-null int64
1 SUV 387 non-null int64
2 Wagon 387 non-null int64
3 Minivan 387 non-null int64
4 Pickup 387 non-null int64
5 AWD 387 non-null int64
6 RWD 387 non-null int64
7 Retail 387 non-null int64
8 Dealer 387 non-null int64
9 Engine 387 non-null float64
10 Cylinders 387 non-null int64
11 Horsepower 387 non-null int64
12 CityMPG 387 non-null int64
13 HighwayMPG 387 non-null int64
14 Weight 387 non-null int64
15 Wheelbase 387 non-null int64
16 Length 387 non-null int64
17 Width 387 non-null int64
dtypes: float64(1), int64(17)
memory usage: 57.4+ KB
| Acura 3.5 RL | Acura 3.5 RL Navigation | Acura MDX | Acura NSX S | Acura RSX | |
|---|---|---|---|---|---|
| Sports | 0.0 | 0.0 | 0.0 | 1.0 | 0.0 |
| SUV | 0.0 | 0.0 | 1.0 | 0.0 | 0.0 |
| Wagon | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| Minivan | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| Pickup | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| AWD | 0.0 | 0.0 | 1.0 | 0.0 | 0.0 |
| RWD | 0.0 | 0.0 | 0.0 | 1.0 | 0.0 |
| Retail | 43755.0 | 46100.0 | 36945.0 | 89765.0 | 23820.0 |
| Dealer | 39014.0 | 41100.0 | 33337.0 | 79978.0 | 21761.0 |
| Engine | 3.5 | 3.5 | 3.5 | 3.2 | 2.0 |
| Cylinders | 6.0 | 6.0 | 6.0 | 6.0 | 4.0 |
| Horsepower | 225.0 | 225.0 | 265.0 | 290.0 | 200.0 |
| CityMPG | 18.0 | 18.0 | 17.0 | 17.0 | 24.0 |
| HighwayMPG | 24.0 | 24.0 | 23.0 | 24.0 | 31.0 |
| Weight | 3880.0 | 3893.0 | 4451.0 | 3153.0 | 2778.0 |
| Wheelbase | 115.0 | 115.0 | 106.0 | 100.0 | 101.0 |
| Length | 197.0 | 197.0 | 189.0 | 174.0 | 172.0 |
| Width | 72.0 | 72.0 | 77.0 | 71.0 | 68.0 |
Helper function that performs the scaling and actual PCA.
def do_pca(n_components, data):
X = StandardScaler().fit_transform(data)
pca = PCA(n_components)
X_pca = pca.fit_transform(X)
return pca, X_pca
Helper function that:
- Creates a DataFrame of the PCA results
- Includes feature weights and explained variance
- Visualizes the PCA results
def pca_results(full_dataset, pca, plot=True):
'''
Create a DataFrame of the PCA results
Includes dimension feature weights and explained variance
Visualizes the PCA results
'''
# Dimension indexing
dimensions = dimensions = \
['Dimension {}'.format(i) for i in range(1,len(pca.components_)+1)]
# PCA components
components = pd.DataFrame(np.round(pca.components_, 4), columns = full_dataset.keys())
components.index = dimensions
# PCA explained variance
ratios = pca.explained_variance_ratio_.reshape(len(pca.components_), 1)
variance_ratios = pd.DataFrame(np.round(ratios, 4), columns = ['Explained Variance'])
variance_ratios.index = dimensions
if plot:
# Create a bar plot visualization
fig, ax = plt.subplots(figsize = (14,8))
# Plot the feature weights as a function of the components
components.plot(ax = ax, kind = 'bar');
ax.set_ylabel("Feature Weights")
ax.set_xticklabels(dimensions, rotation=0)
# Display the explained variance ratios
for i, ev in enumerate(pca.explained_variance_ratio_):
ax.text(i-0.40, ax.get_ylim()[1] + 0.05,
"Explained Variance\n %.4f"%(ev))
# Return a concatenated DataFrame
return pd.concat([variance_ratios, components], axis = 1)
For context, as outlined in my other notes on PCA:
- Principal components span the directions of maximum variability.
- Principal components are always orthogonal to one another.
- Eigenvalues tell us the amount of information a principal component holds.
First, consider the first 3 principal components:
pca, X_pca = do_pca(3, c)
pca_results(c, pca).T
| Dimension 1 | Dimension 2 | Dimension 3 | |
|---|---|---|---|
| Explained Variance | 0.4352 | 0.1667 | 0.1034 |
| Sports | -0.0343 | 0.4420 | 0.0875 |
| SUV | -0.1298 | -0.2261 | 0.4898 |
| Wagon | 0.0289 | -0.0106 | 0.0496 |
| Minivan | -0.0481 | -0.2074 | -0.2818 |
| Pickup | 0.0000 | -0.0000 | 0.0000 |
| AWD | -0.0928 | -0.1447 | 0.5506 |
| RWD | -0.1175 | 0.3751 | -0.2416 |
| Retail | -0.2592 | 0.3447 | 0.0154 |
| Dealer | -0.2576 | 0.3453 | 0.0132 |
| Engine | -0.3396 | 0.0022 | -0.0489 |
| Cylinders | -0.3263 | 0.0799 | -0.0648 |
| Horsepower | -0.3118 | 0.2342 | 0.0040 |
| CityMPG | 0.3063 | 0.0169 | -0.1421 |
| HighwayMPG | 0.3061 | 0.0433 | -0.2486 |
| Weight | -0.3317 | -0.1832 | 0.0851 |
| Wheelbase | -0.2546 | -0.3066 | -0.2846 |
| Length | -0.2414 | -0.2701 | -0.3361 |
| Width | -0.2886 | -0.2163 | -0.1369 |
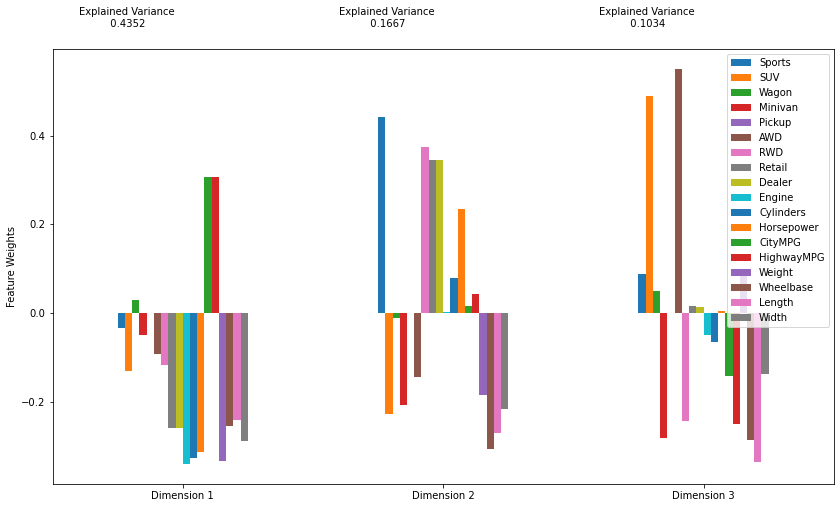
print('Number of Components : Variance Explained')
for component_count in range(1,17):
pca, X_pca = do_pca(component_count, c)
results = pca_results(c, pca, False)
print('{:20} : {:2.1%}'.format(component_count,
results['Explained Variance'].sum()))
Number of Components : Variance Explained
1 : 43.5%
2 : 60.2%
3 : 70.5%
4 : 76.8%
5 : 82.4%
6 : 86.8%
7 : 89.7%
8 : 92.5%
9 : 95.0%
10 : 96.8%
11 : 97.7%
12 : 98.5%
13 : 99.0%
14 : 99.5%
15 : 99.8%
16 : 100.0%
Note that the first two components, alone, account for 60% of the variance in the dataset.
This content is taken from notes I took while pursuing the Intro to Machine Learning with Pytorch nanodegree certification.