DBSCAN
This notebook demonstrates using DBSCan to cluster a couple of datasets. It shows how changing its parameters (epsilon and min_samples) changes the resulting cluster structure.
import pandas as pd
import matplotlib.pyplot as plt
from itertools import cycle, islice
import numpy as np
from sklearn import cluster
Helper Function to Plot Datasets
figsize = (10,10)
point_size=150
point_border=0.8
def plot_dataset(dataset, xlim=(-15, 15), ylim=(-15, 15)):
plt.figure(figsize=figsize)
plt.scatter(dataset[:,0], dataset[:,1], s=point_size,
color="#00B3E9", edgecolor='black', lw=point_border)
plt.xlim(xlim)
plt.ylim(ylim)
plt.show()
Blobs Dataset
Open first several points in the blobs dataset.
blobs = pd.read_csv('dbscan/blobs.csv')[:80].values
blobs[:5]
array([[ 8.62218539, 1.93579579],
[-4.73670958, -7.97095765],
[ 9.62122205, 0.92542315],
[ 6.16209503, -0.27325437],
[ 8.69748809, -1.05745206]])
plot_dataset(blobs)

Helper Function to Plot Clusters
def plot_clustered_dataset(dataset, y_pred, xlim=(-15, 15), ylim=(-15, 15),
neighborhood=False, epsilon=0.5, min_samples=5):
fig, ax = plt.subplots(figsize=figsize)
colors = np.array(list(islice(cycle(['#df8efd', '#78c465', '#ff8e34',
'#f65e97', '#a65628', '#984ea3',
'#999999', '#e41a1c', '#dede00']),
int(max(y_pred) + 1))))
colors = np.append(colors, '#BECBD6')
if neighborhood:
for point in dataset:
circle1 = plt.Circle(point, epsilon, color='#666666',
fill=False, zorder=0, alpha=0.3)
ax.add_artist(circle1)
ax.scatter(dataset[:, 0], dataset[:, 1], s=point_size,
color=colors[y_pred], zorder=10,
edgecolor='black', lw=point_border)
plt.xlim(xlim)
plt.ylim(ylim)
plt.title('Epsilon: {}, Min_Samples: {}'.format(epsilon, min_samples))
plt.show()
Create and fit DBSCAN
dbscan = cluster.DBSCAN()
clustering_labels_1 = dbscan.fit_predict(blobs)
plot_clustered_dataset(blobs, clustering_labels_1)
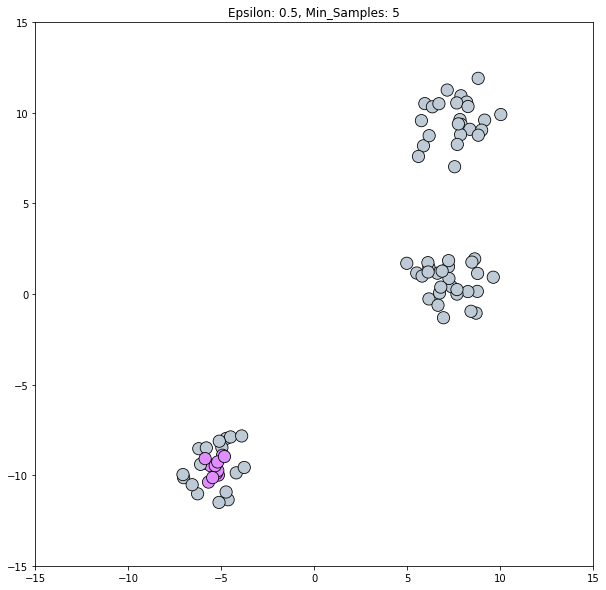
Plot Epsilon, the radius of each point’s neighborhood. The default value in sklearn is 0.5.
plot_clustered_dataset(blobs, clustering_labels_1, neighborhood=True)
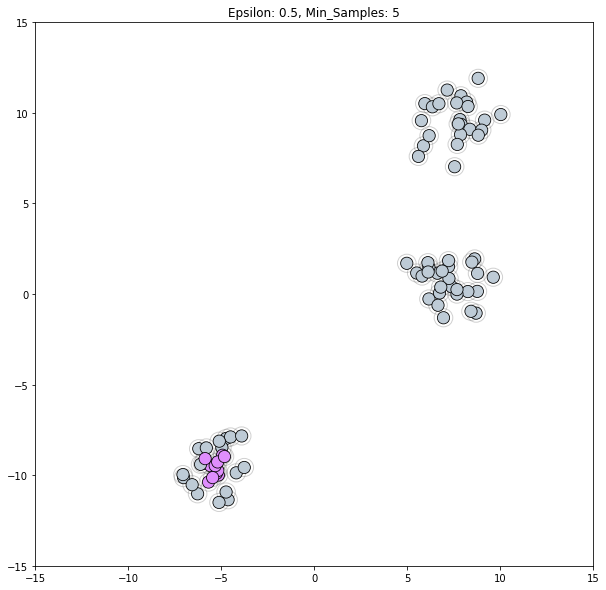
We can see that an Epsilon value of 0.5 is too small for this dataset. We need to increase it such that points in a blob overlap each others' neighborhoods, but not to the degree where a single cluster would pan two blobs.
for epsilon in [1, 1.5, 2, 5, 6]:
dbscan = cluster.DBSCAN(eps=epsilon)
clustering_labels_2 = dbscan.fit_predict(blobs)
plot_clustered_dataset(blobs, clustering_labels_2, neighborhood=True,
epsilon=epsilon)

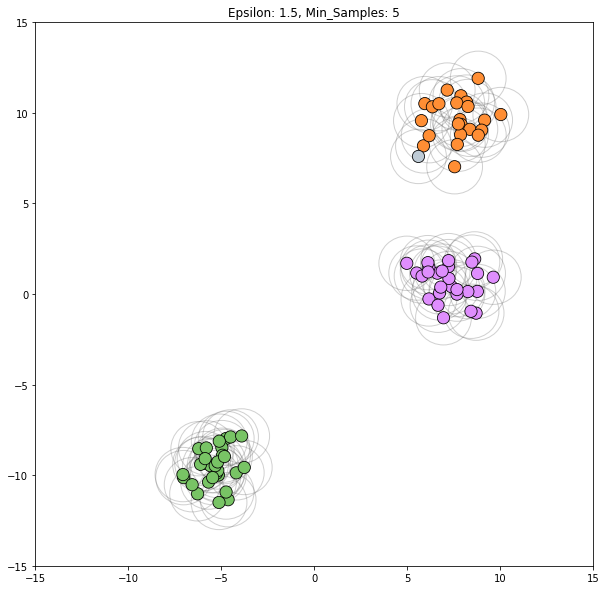
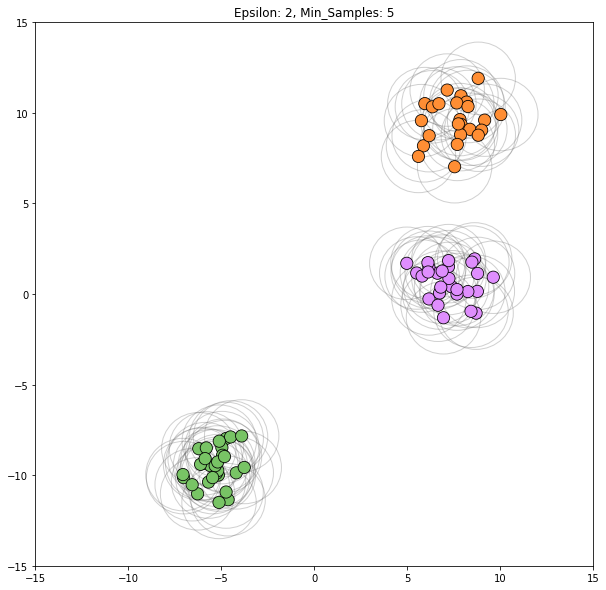

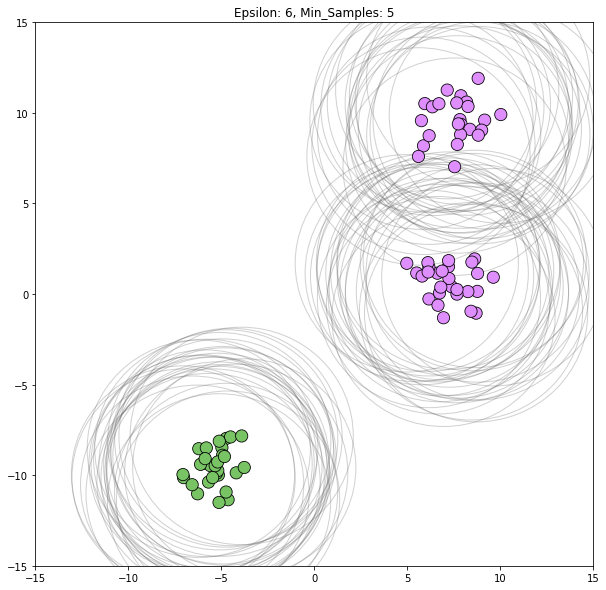
Epsilon values from 2 through 5 all appear viable to correctly classify this dataset.
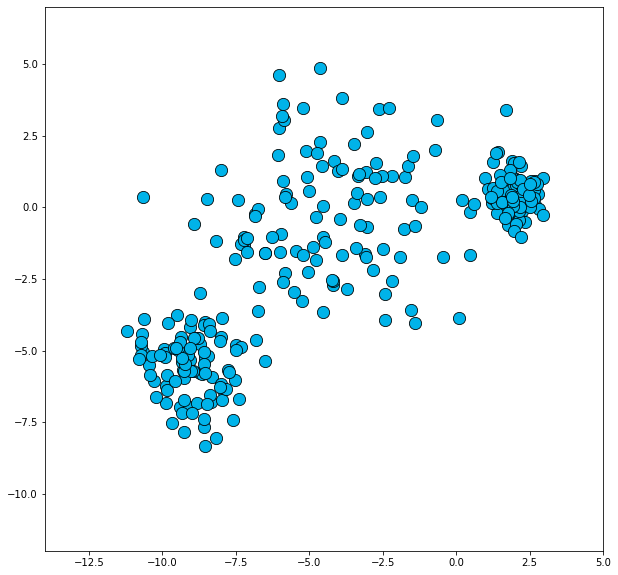
Varied Dataset
varied = pd.read_csv('dbscan/varied.csv')[:300].values
plot_dataset(varied, xlim=(-14, 5), ylim=(-12, 7))
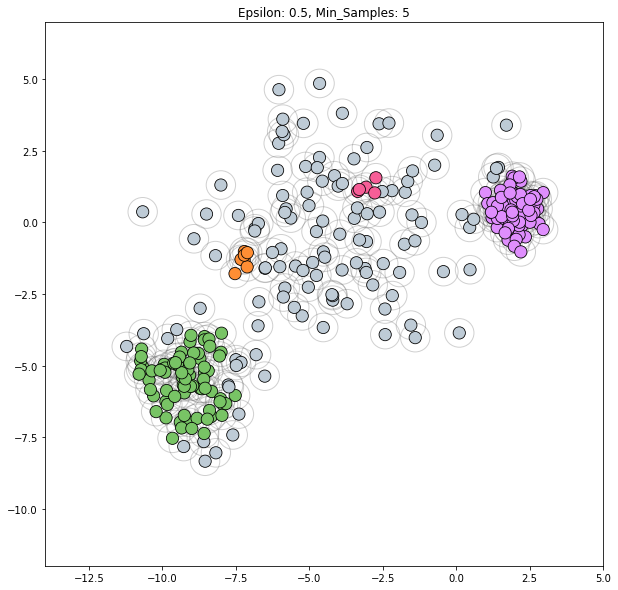
dbscan = cluster.DBSCAN()
clustering_labels_3 = dbscan.fit_predict(varied)
plot_clustered_dataset(varied, clustering_labels_3,
xlim=(-14, 5), ylim=(-12, 7),
neighborhood=True, epsilon=0.5)
Try to plot two scenarios:
Scenario 1: 3 clusters: left blob, right blob, central area
Scenario 2: 2 clusters: left blob, right blob
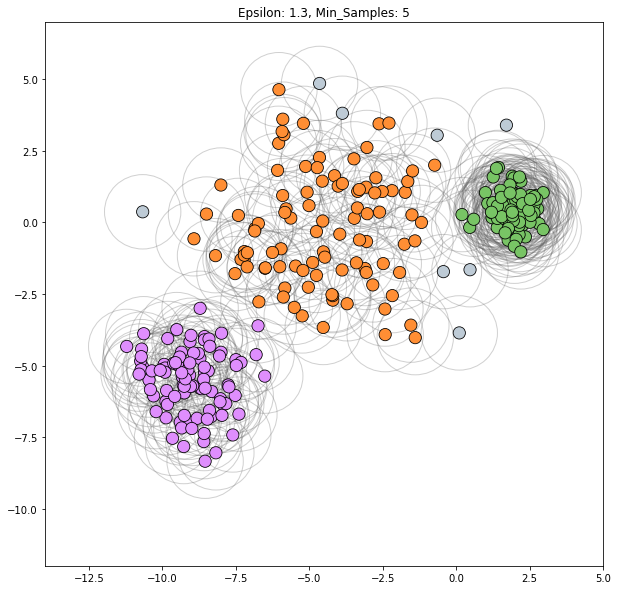
Scenario 1
3 clusters: left blob, right blob, central area
epsilon = 1.3
min_samples=5
dbscan = cluster.DBSCAN(eps=epsilon, min_samples=min_samples)
clustering_labels_3 = dbscan.fit_predict(varied)
plot_clustered_dataset(varied, clustering_labels_3,
xlim=(-14, 5), ylim=(-12, 7),
neighborhood=True, epsilon=epsilon,
min_samples=min_samples)
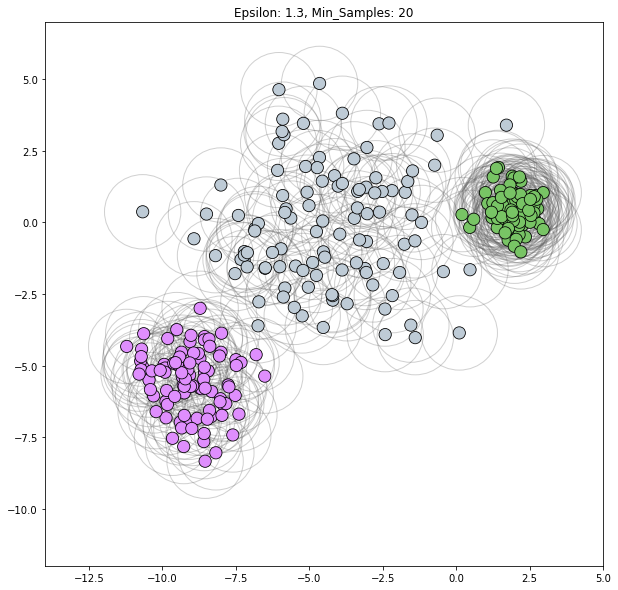
Scenario 2
2 clusters: left blob, right blob
epsilon = 1.3
min_samples=20
dbscan = cluster.DBSCAN(eps=epsilon, min_samples=min_samples)
clustering_labels_3 = dbscan.fit_predict(varied)
plot_clustered_dataset(varied, clustering_labels_3,
xlim=(-14, 5), ylim=(-12, 7),
neighborhood=True, epsilon=epsilon,
min_samples=min_samples)
Helper function to plot grid
def plot_dbscan_grid(dataset, eps_values, min_samples_values):
fig = plt.figure(figsize=(16, 20))
plt.subplots_adjust(left=.02, right=.98, bottom=0.001, top=.96, wspace=.05,
hspace=0.25)
plot_num = 1
for i, min_samples in enumerate(min_samples_values):
for j, eps in enumerate(eps_values):
ax = fig.add_subplot( len(min_samples_values) , len(eps_values), plot_num)
dbscan = cluster.DBSCAN(eps=eps, min_samples=min_samples)
y_pred_2 = dbscan.fit_predict(dataset)
colors = np.array(list(islice(cycle(['#df8efd', '#78c465', '#ff8e34',
'#f65e97', '#a65628', '#984ea3',
'#999999', '#e41a1c', '#dede00']),
int(max(y_pred_2) + 1))))
colors = np.append(colors, '#BECBD6')
for point in dataset:
circle1 = plt.Circle(point, eps, color='#666666',
fill=False, zorder=0, alpha=0.3)
ax.add_artist(circle1)
ax.text(0, -0.03, 'Epsilon: {} \nMin_samples: {}'.format(eps, min_samples),
transform=ax.transAxes, fontsize=16, va='top')
ax.scatter(dataset[:, 0], dataset[:, 1], s=50, color=colors[y_pred_2],
zorder=10, edgecolor='black', lw=0.5)
plt.xticks(())
plt.yticks(())
plt.xlim(-14, 5)
plt.ylim(-12, 7)
plot_num = plot_num + 1
plt.show()
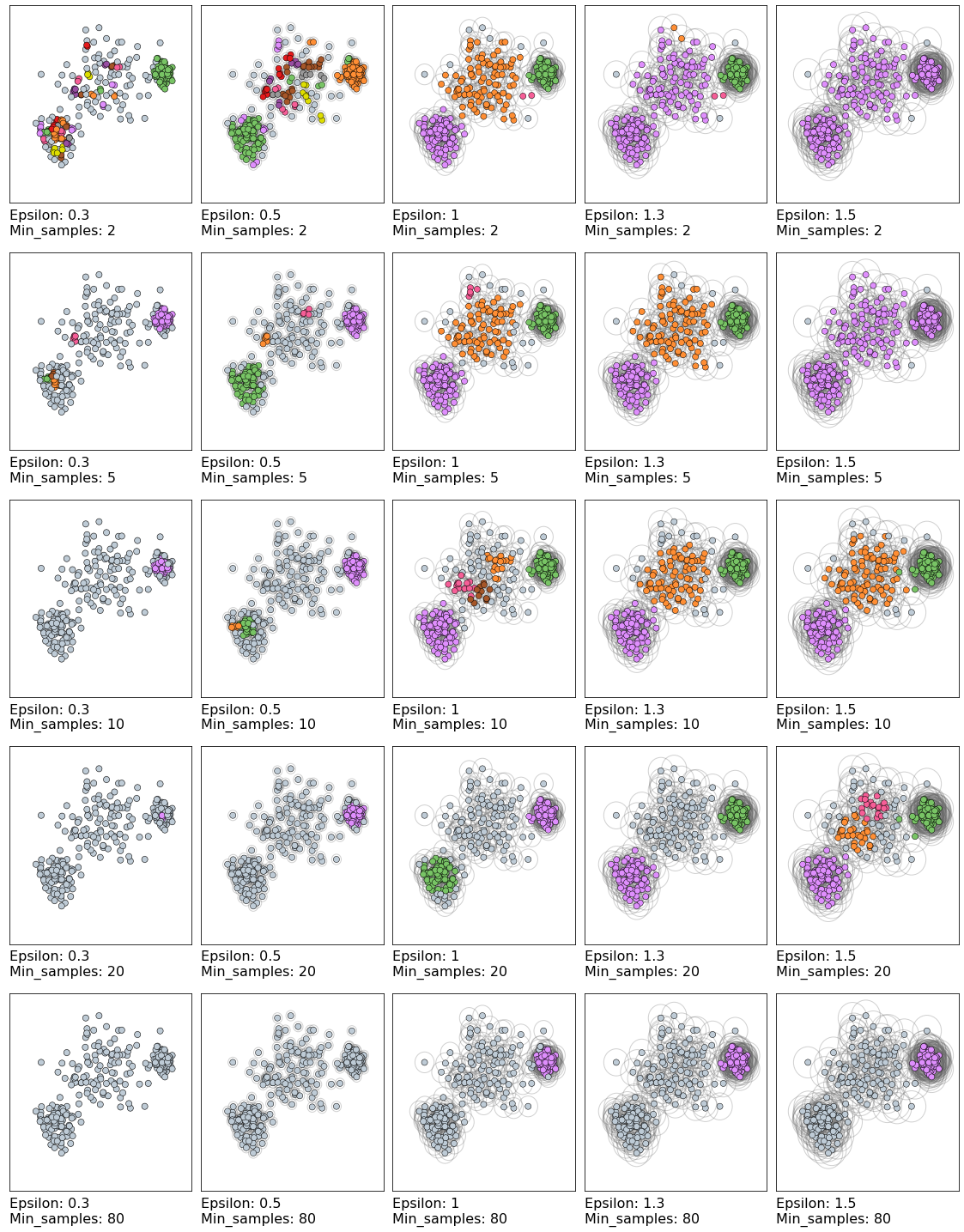
Show Grid
The following grid plots the DBSCAN clustering results of a range of parameter values.
Epsilon varies horizontally, while vertically each row shows a different value of min_samples.
eps_values = [0.3, 0.5, 1, 1.3, 1.5]
min_samples_values = [2, 5, 10, 20, 80]
plot_dbscan_grid(varied, eps_values, min_samples_values)
Heuristics
If most/all data points are labeled as noise excpt for extremely dense regions, decrease epsilon and decrease min_samples
If most points belong to one cluster, decrease epsilon and increase min_samples
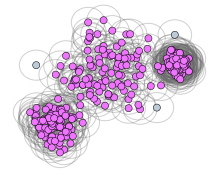
If most or all data points are labeled as noise, increase epsilon and decrease min_samples
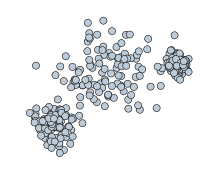
If there are many small clusters (more than expected for the dataset), increase epsilon and increase min_samples