Regression Model Evaluation

There are several metrics we can use to evaluate regression models:

• Mean Absolute Error
• Mean Squared Error
• R2 Score

Mean Absolute Error

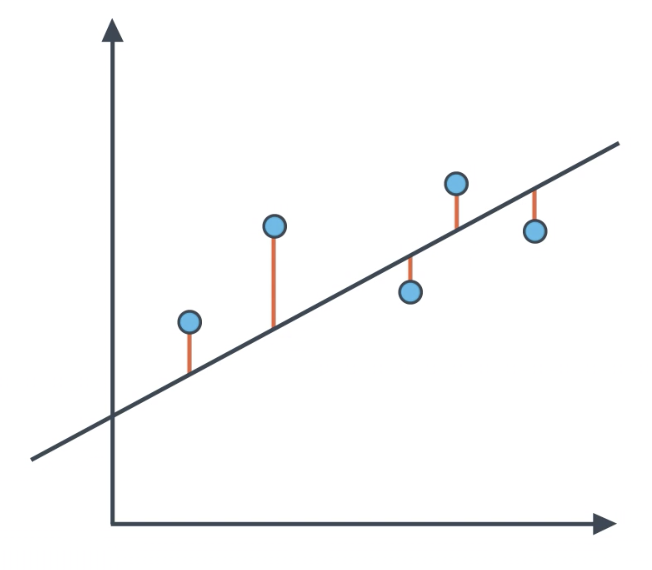
The Mean Absolute Error, is the sum of the absolute values of the distances from the points to the line.

import numpy as np

from sklearn.metrics import mean_absolute_error
from sklearn.linear_model import LinearRegression

X = np.array([1, 2, 3, 3, 4]).reshape(-1,1)
y = np.array([3, 4, 3, 4, 3]).reshape(-1,1)

classifier = LinearRegression()
classifier.fit(X,y)

guesses = classifier.predict(X)

mean_absolute_error(y, guesses)

0.476923076923077

Mean Absolute Error can also be implemented manually, as follows:

def mae(actual, preds):
    return np.sum(abs(actual - preds))/len(actual)

mae(y, guesses)

0.476923076923077

Mean Squared Error

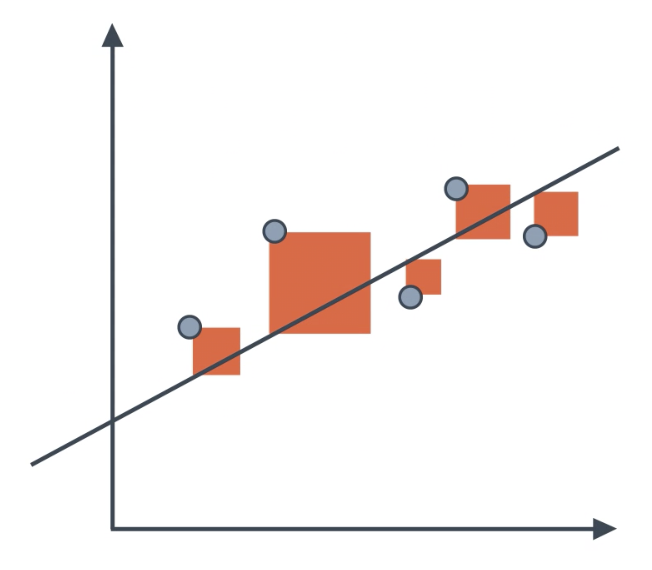
One problem with mean absolute error is that the absolute value function is not differentiable. This a problem if we intend to us methods such as gradient descent. To solve this problem, we use the more common Mean Squared Error.

Note that optimizing on the mean squared error will always lead to the same ‘best’ model as if you were to optimize on the r2 value. The mean squared error is by far the most used metric for optimization in regression problems.

MSE can be thought of as the average amount that you miss by across all the points.

from sklearn.metrics import mean_squared_error
from sklearn.linear_model import LinearRegression

classifier = LinearRegression()
classifier.fit(X,y)

guesses = classifier.predict(X)

mean_squared_error(y, guesses)

0.23846153846153856

Mean Squared Error can also be implemented manually, as follows:

def mse(actual, preds):
    return np.sum((actual - preds)**2)/len(actual)

mse(y, guesses)

0.23846153846153856

R2 Score

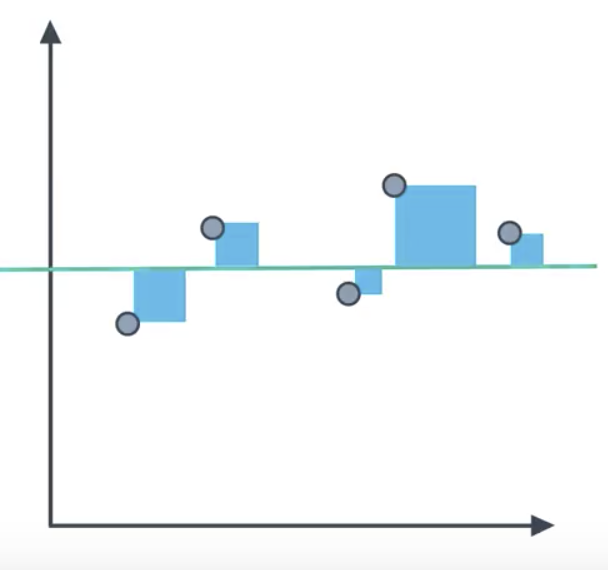
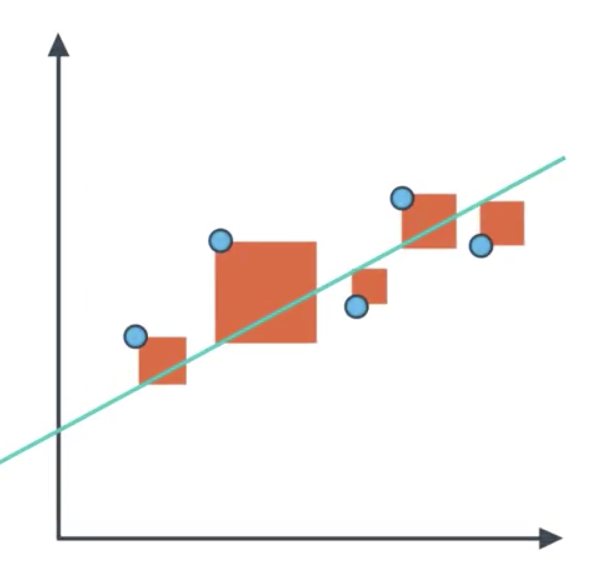
The R2 Score is based on comparing our model to the simplest possible model: a horizontal line. Drawing this horizontal line is straightforward, as it only requires taking the average of the y-values of the points. Reasonable regression models will have mean-squared-error smaller than that of the simple model. We calculate the ratio of the former to the latter, and sutract the result from 1.

$$R2 = 1-\frac{regression_{mean\ squared\ error}}{horizontal\ line_{mean\ squared\ error}}$$

• Bad model: R2 will be close to 0.
• Good model: R2 will be close to 1.

Note that optimizing on the mean squared error will always lead to the same ‘best’ model as if you were to optimize on the r2 value.

The R2 value is frequently interpreted as the ‘amount of variability’ captured by a model.

from sklearn.metrics import r2_score

y_true = np.array([1, 2, 4]).reshape(-1,1)
y_pred = np.array([1.3, 2.5, 3.7]).reshape(-1,1)

r2_score(y_true, y_pred)

0.9078571428571429

The R2 Score can also be implemented manually, as follows:

def r2(actual, preds):
    sse = np.sum((actual-preds)**2)
    sst = np.sum((actual-np.mean(actual))**2)
    return 1 - sse/sst

r2(y_true, y_pred)

0.9078571428571429

Boston Housing Example

• Linear Regression is one of very few machine learning models that should not be used for classification (predicting categories for data).
• Logistic Regression, on the other hand, cannot be used to predict numeric categories.
• Most sklearn models can be used for both regression and classification, including Decision Trees, Random Forest, and Adaptive Boosting.

Each of these model except logistic regression will be used to perform regression on the Boston Housing Dataset.

from sklearn.datasets import load_boston
from sklearn.model_selection import train_test_split
import numpy as np

boston = load_boston()
y = boston.target
X = boston.data

X_train, X_test, y_train, y_test = train_test_split(
            X, y, test_size=0.33, random_state=42)

Import modules.

from sklearn.tree import DecisionTreeRegressor
from sklearn.ensemble import RandomForestRegressor
from sklearn.ensemble import AdaBoostRegressor
from sklearn.linear_model import LinearRegression

Instantiate models.

decision_tree = DecisionTreeRegressor()
random_forest = RandomForestRegressor()
adaboost = AdaBoostRegressor()
linear = LinearRegression()

Fit data.

decision_tree.fit(X_train,y_train)
random_forest.fit(X_train,y_train)
adaboost.fit(X_train,y_train)
linear.fit(X_train,y_train);

Make predictions on the test data.

decision_tree_preds = decision_tree.predict(X_test)
random_forest_preds = random_forest.predict(X_test)
adaboost_preds = adaboost.predict(X_test)
linear_preds = linear.predict(X_test)

Print the metrics for each of these models.

for label, preds in [('Decision Tree', decision_tree_preds),
                     ('Random Forest', random_forest_preds),
                     ('Adaboost',      adaboost_preds),
                     ('Linear',        linear_preds)]:
    
    r2 = r2_score(y_test, preds)
    mse = mean_squared_error(y_test, preds)
    mae = mean_absolute_error(y_test, preds)

    print('\n  --- {} ---'.format(label))
    print('           R2 Score: {:.3}'.format(r2))
    print(' Mean Squared Error: {:.3}'.format(mse))
    print('Mean Absolute Error: {:.3}'.format(mae))

  --- Decision Tree ---
           R2 Score: 0.762
 Mean Squared Error: 18.0
Mean Absolute Error: 2.89

  --- Random Forest ---
           R2 Score: 0.864
 Mean Squared Error: 10.3
Mean Absolute Error: 2.12

  --- Adaboost ---
           R2 Score: 0.789
 Mean Squared Error: 16.0
Mean Absolute Error: 2.75

  --- Linear ---
           R2 Score: 0.726
 Mean Squared Error: 20.7
Mean Absolute Error: 3.15

The Random Forest regressor was the top performer across all metrics.