Perceptron
Perceptrons are the basis of neural networks. They exist to perform classifications like that shown below. Each dot represents the test scores and grades for set of students applying to a university. Blue dots indicate the student was accepted to the university. Red indicates they were denied.
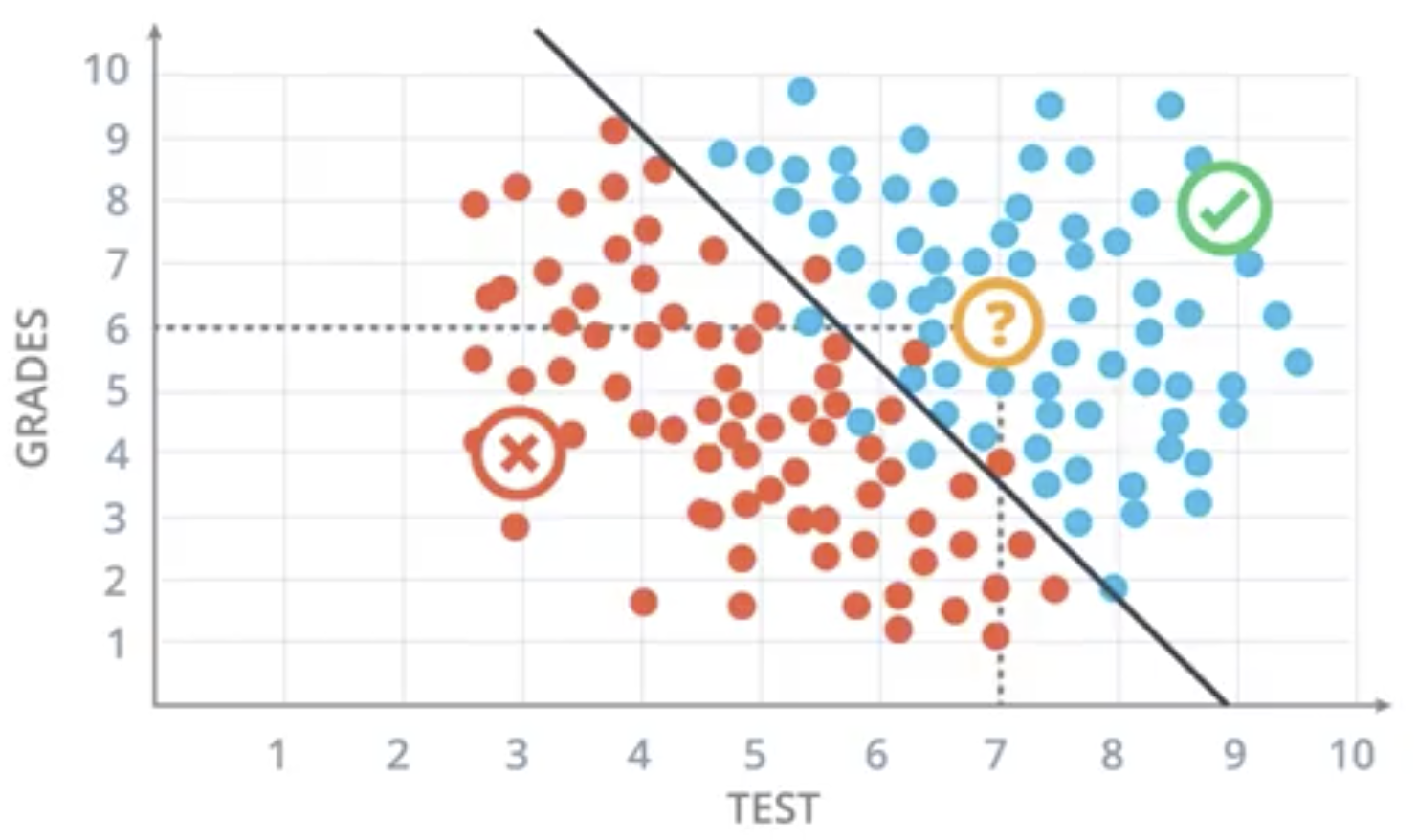
In the case of the dot in yellow, above, we would assume they were accepted given that they are above the black dividing line.
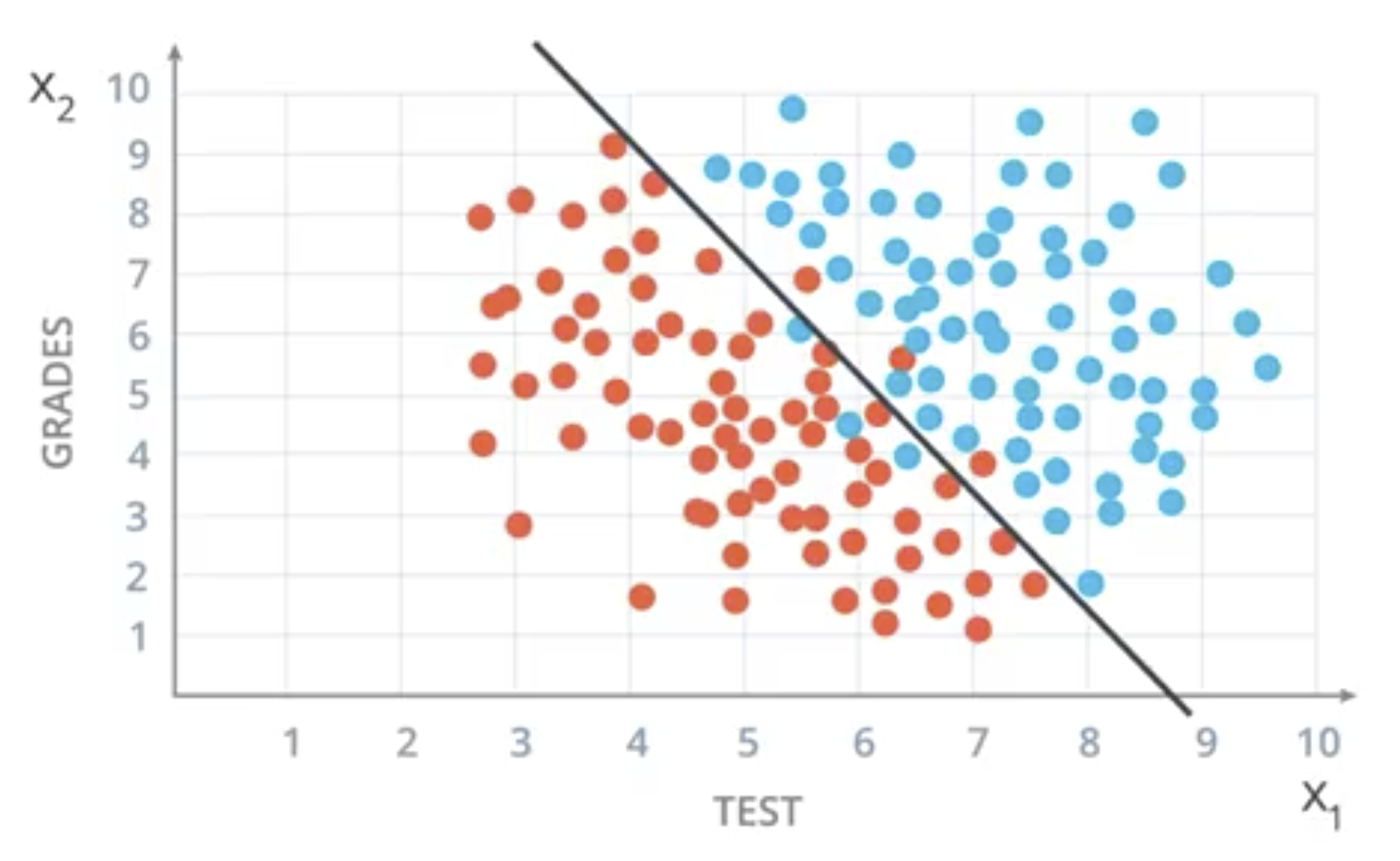
The formula for the black line is given by:
$$2 x_1 + x_2 - 18 = 0$$
Algorithmically, we could assign each applying student a score based on the following formula:
$$Score = 2(Test) + Grades - 18$$
- If score > 0, the student is Accepted.
- If score < 0, the student is Denied.
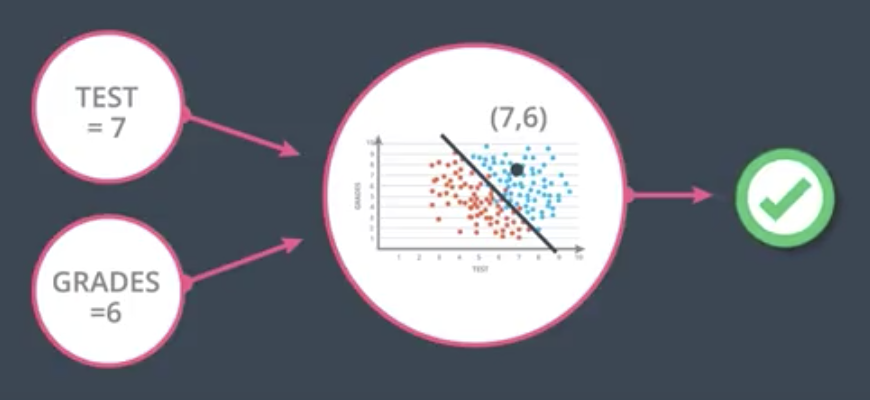
In the example student above (Test = 7, Grades = 6), their score comes out to 2, which means they would be Accepted.
General Form for 2 Dimensions
The more general equation for a 2-dimensional boundary line is the following.
$$w_1 x_1 + w_2 x_2 + b = 0$$
This can also be expressed as
$$ Wx + b = 0,\ where\ W = (w_1, w_2),\ x = (x_1, x_2)$$
$$\hat{y} = 1,\ if Wx + b \geq 0$$ $$\hat{y} = 0,\ Wx + b < 0$$
The goal of the algorithm is to have $y$ the same as $\hat{y}$ as often as possible.
More General Case
The more general case exists in $n$-dimensional space where each point ($x_1, x_2, …, x_n$) is either above or below an n-1 dimensional hyperplane. The equation of the hyperplane is still $Wx+b=0$.
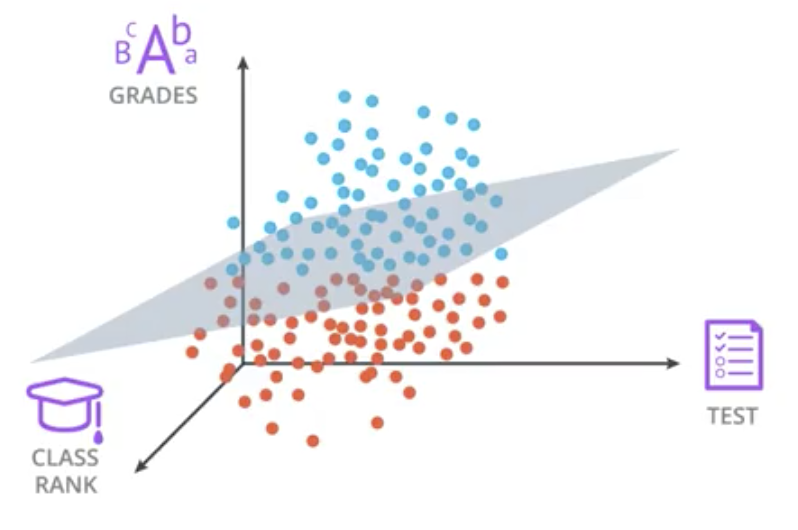
To satisfy this equation, the weights, $W$, will be a $(1 \times n)$ vector, the input features, $x$, will be $(n \times 1)$, and the bias, $b$, will be $(1 \times 1)$.
Perceptron
A perceptron is an encoding of our equation above into a small graph. The perceptron receives the points as inputs, like in the image below, and returns $1$ if the point is in the positive area, and a $0$ otherwise.
The bias can be thought of as another input with magnitude 1 and edge weight equal to the bias term, as show below.
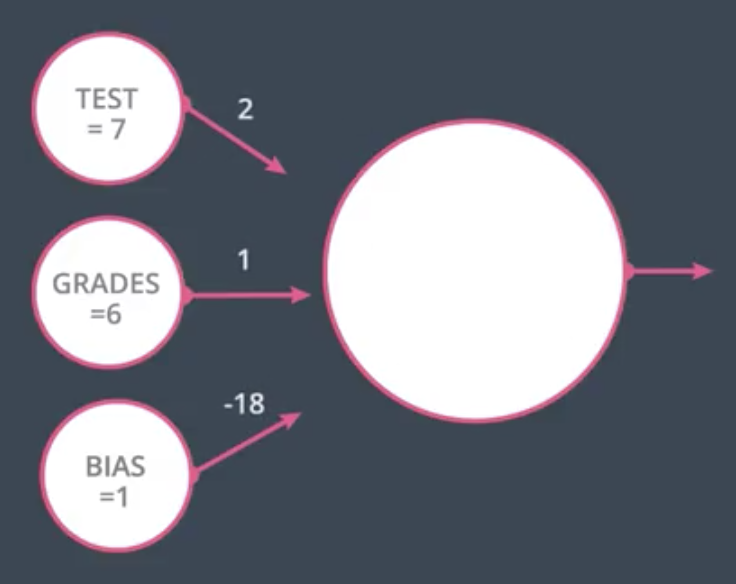
In the case of the example above:
$$Score = 2 \times 7 + 1 \times 6 - 18 \times 1 = 2$$
Since $2 \geq 0$, the perceptron would output $1$.
The more general case of a perceptron with $n$ inputs is shown below.
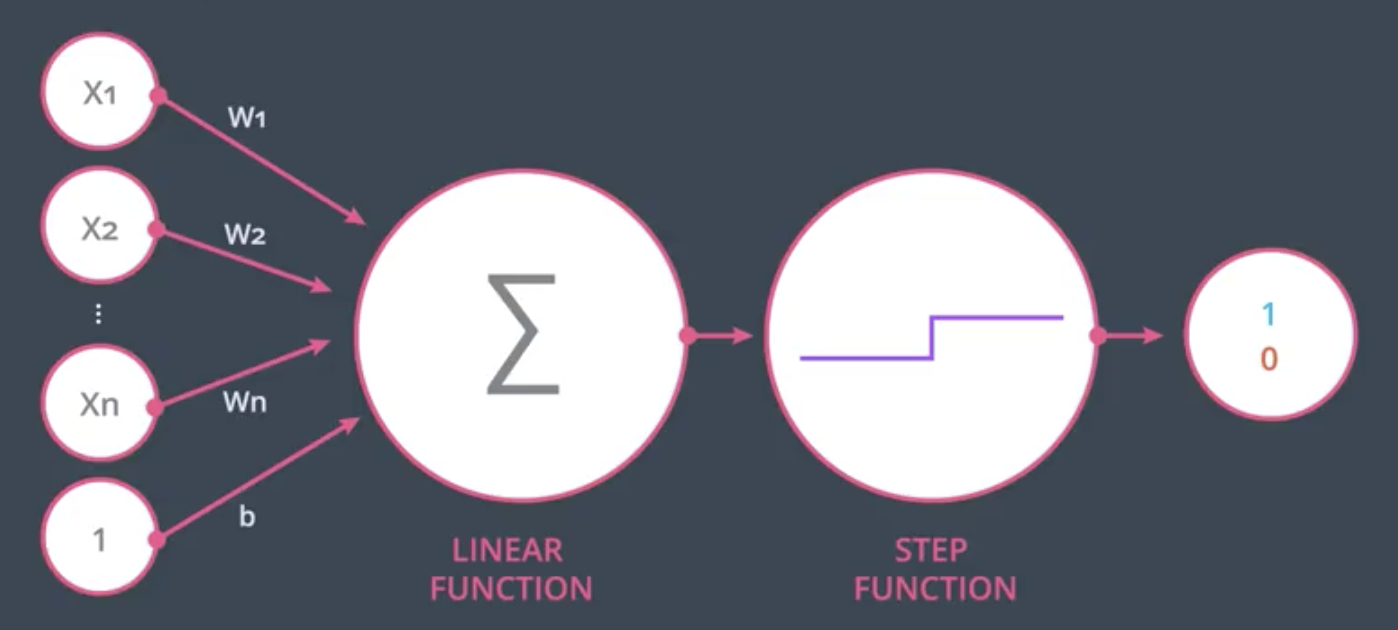
During the linear function part of the node above, the node calculates $Wx + b = \sum^n_{i=1} W_i X_i + b$. The output of that linear function is run through a step function during which the continuous output of the linear function is categorized into a binary $1$ or $0$.
Perceptrons as Logical Operators
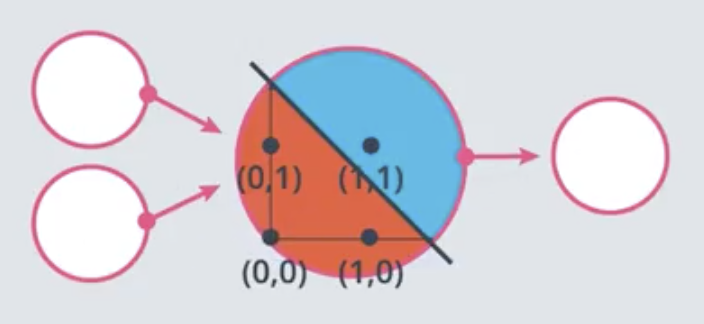
By setting the weights and bias strategically, perceptrons can be made to function as logical operators. The perceptron below functions as an AND operator.
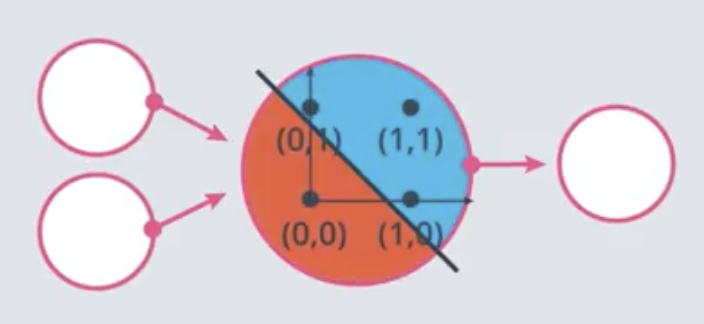
This one functions as an OR.
A perceptron that models NOT can also be constructed. Combinations of AND, OR, and NOT perceptrons can be used to create more complicated logical operators such as NAND and XOR.
Perceptron Trick
The perceptron trick involves moving the line progressively closer to any misclassified points. For example, in the following image the point $(4,5)$ is misclassified on the wrong side of the boundary line $3x_1 + 4x_2 - 10 = 0$.
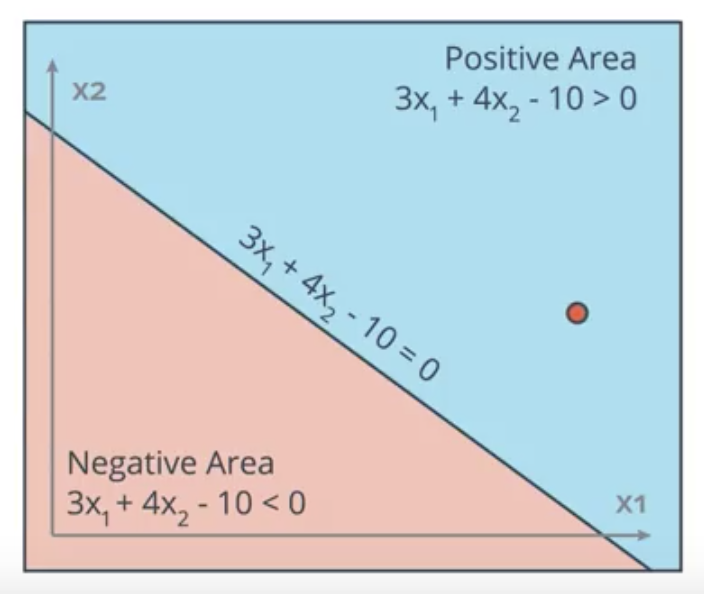
To adjust the location of the line, it is adjusted by a small rate-limiting factor (“learning rate”) times the location of the point, with a 1 added as the bias. The line $3x_1 + 4x_2 - 10 = 0$ could be denoted by the tuple $(3, 4, -10)$ and the point denoted by $(4, 5, 1)$. For a learning rate of $0.1$, the adjusted equation of the line would be:
$$(3, 4, -10) - 0.1(4, 5, 1) = (2.6, 3.5, 10.1)$$
Thus, the new equation for the line is $2.6x_1 + 3.5x_2 - 10.1 = 0$.
Perceptron Algorithm
- Start with random weights: $w_1, …, w_n, b$
For every misclassified point $(x_1, …, x_n)$:
2.1. If prediction = 0:
- For i = 1 … n:
- Change $w_i \rightarrow w_i + \alpha x_i$
- Change $b \rightarrow b + \alpha$
2.2 If prediction = 1:
- For i = 1 … n:
- Change $w_i = w_i - \alpha x_i$
- Change $b \rightarrow b - \alpha$
- For i = 1 … n: