Perceptron Implementations

%matplotlib inline
%config InlineBackend.figure_format = 'retina'

import numpy as np
np.random.seed(42)
import matplotlib.pyplot as plt

def stepFunction(t):
    if t >= 0:
        return 1
    return 0

def prediction(X, W, b):
    return stepFunction((np.matmul(X,W)+b)[0])

def perceptronStep(X, y, W, b, learn_rate = 0.01):
    for i in range(len(X)):
        y_hat = prediction(X[i],W,b)
        if y[i]-y_hat == 1:
            W[0] += X[i][0]*learn_rate
            W[1] += X[i][1]*learn_rate
            b += learn_rate
        elif y[i]-y_hat == -1:
            W[0] -= X[i][0]*learn_rate
            W[1] -= X[i][1]*learn_rate
            b -= learn_rate
    return W, b

def trainPerceptronAlgorithm(X, y, learn_rate = 0.01, num_epochs = 40):
    x_min, x_max = min(X.T[0]), max(X.T[0])
    y_min, y_max = min(X.T[1]), max(X.T[1])
    W = np.array(np.random.rand(2,1))
    b = np.random.rand(1)[0] + x_max
    boundary_lines = []
    for i in range(num_epochs):
        # In each epoch, we apply the perceptron step.
        W, b = perceptronStep(X, y, W, b, learn_rate)
        boundary_lines.append((-W[0]/W[1], -b/W[1]))
    return boundary_lines

data = np.loadtxt('perceptron-implementations/data.csv', 
                  delimiter = ',')

X = data[:,:-1]
y = data[:,-1]

lines = trainPerceptronAlgorithm(X, y)

print('Epoch :\t\tW\t\tB')
for n, line in enumerate(lines):
    print('{}:\t\t{}\t\t{}'
          .format(str(n+1).zfill(2),
                  round(line[0][0],3), 
                  round(line[1][0],3)))

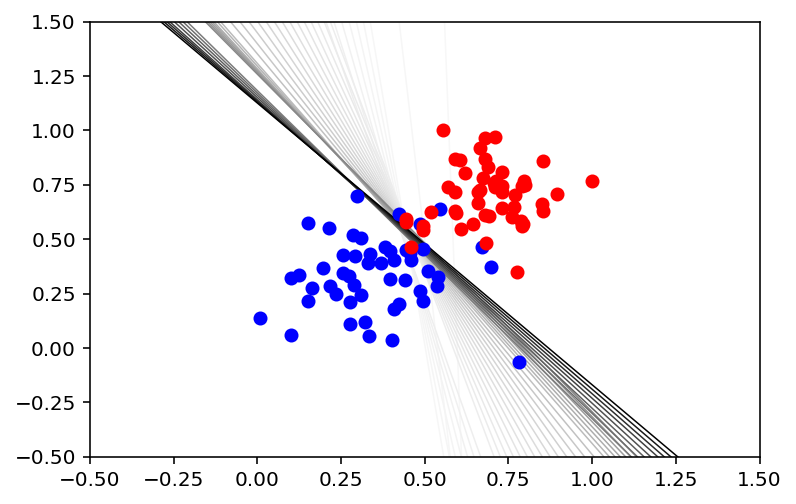
plt.figure()

X_min = X[:,:1].min()
X_max = X[:,:1].max()

counter = len(lines)
for w, b in lines:
    counter -= 1
    color = [1 - 0.91 ** counter for _ in range(3)]
    plt.plot([X_min-0.5, X_max+0.5],
             [(X_min-0.5) * w + b, (X_max+0.5) * w + b],
             color=color,
             linewidth=0.75)
    
plt.scatter(X[:50,:1], 
            X[:50,1:], 
            c = 'blue',
            zorder=3)
plt.scatter(X[50:,:1], 
            X[50:,1:], 
            c = 'red',
            zorder=3)

plt.gca().set_xlim([-0.5,1.5])
plt.gca().set_ylim([-0.5,1.5]);