How Google does Machine Learning
Introduction
This particular section is a discussion of the ML know-how Google has acquired. According to Josh, Google has created more value-added ML models than any other company. The perspective of this section is that a business leader would take on Machine Learning.
ML Surprise
What is ML? Machine learning is the process of a computer writing a computer program to accomplish a task. A computer figures out the “best” program to write by only looking at a set of examples.
How does this compare to traditional software engineering? Software engineers are humans that write programs that transform inputs to outputs.
Building an end-to-end ML system requires the following five tasks:
- Defining KPIs (Key Performance Indicators) - what you are trying to accomplish
- Collecting Data
- Building Infrastructure
- Optimizing ML Algorithm
- Integration - integrating with the rest of the pre-existing systems in the organization
| Task | Expectation | Reality |
|---|---|---|
| Defining KPIs | 15% | 10% |
| Collecting Data | 10% | 30% |
| Building Infrastructure | 10% | 30% |
| Optimizing ML Algorithms | 60% | 10% |
| Integration | 5% | 20% |
According to Josh, optimizing the ML algorithm takes much less time than people expect. But, he’s never seen someone overestimate how hard it will be to get the data right in the first place. And, organizations should be very conscious of how difficult it may be to serve the model at scale, and to train the model in a time efficient manner, so that the model can be iterated on. It is the software tasks that end up taking a lot of time investment to get right. The other insight Josh offers is that frequently simply investing the time doing the ordinary tasks up front may result in ML being less necessary than originally conceived, but the business will still benefit from going through the exercise of preparing for ML.
So the ML surprise is that the actual ML is less important than most people initially conceive. Why learn ML if the ML is not as important as many think? Because the path to ML creates value, at all stages along that path.
The Secret Sauce
The secret sauce Google shares in this section is the organizational know-how it has acquired over many years of managing more value-generating ML systems than any company in the world. Google’s expressed desire for this series of courses is to make the people who complete it great “ML strategists,” above all else. But, the technical ML skills required for ML consist primarily in software and data handling skills.
Josh presents a list of 10 ML pitfalls organizations face when trying to adopt ML. Josh has aggregated these informally, based upon the accumulated know-how Google has accrued.
-
ML requires just as much software infrastructure [as a simpler software solution]
The misconception is that training an ML system would be faster than writing the software. Actual ML systems require significant investment in software stacks surrounding it to ensure it is robust, scalable, and has good up-time. These investments have to be made for software anyway, and then there is the additional complexity associated with data collection, training, etc. Bottom line, ML takes longer and is more complex to develop than a simpler software-only solution, so Google recommends developing the latter prior to trying to develop a full-blow ML system.
-
No data collected yet
You cannot do ML if you do not have the data. Obtaining the data requires significant time and effort investment, and this must be completed first.
-
Assume the data is ready for use
An extension of the previous pitfall is assuming the data is in a format that can be readily used for ML training. Generally, if there is not someone in the organization who is regularly reviewing the data and already using it to generate value, it is not being maintained, and may be "going stale." Josh has never had a client who overestimated the amount of time required to clean data. He says, "expect there to be a lot of pain and friction here."
-
[Forgetting to put and] Keep humans in the loop
As a company's ML initiatives mature, ML can become very integral parts of the business's decision-making processes. To protect these valuable systems, it is necessary to have humans performing sanity checks. These humans should review the data, handle cases where the ML did not perform well, and curate training inputs. Josh says almost ever production ML system at Google has humans in the loop.
-
Product launch focused on the ML algorithm
Users care more about features than underlying technology. Marketing a product based upon the underlying technology may prove a mistake, if the ML proves to be the wrong solution, or performs very poorly.
-
ML optimizing for the wrong thing
Josh presents the example of a Google Search system that optimizes based on clicks, conceived as a proxy for user engagement. The system may "learn" to serve up bad results because that requires users to click more often. Josh warns that ML practitioners need to be very aware of creating "perverse incentives."
-
Is your ML improving things in the real world?
It is helpful to have benchmarks available to gauge actual performance of the new ML system. If there is no baseline user engagement, or baseline performance, it can be difficult to justify additional investment in ML for other projects, because you are unable to demonstrate the value the first system provided.
-
Using a pre-trained ML algorithm versus building your own
Josh warns against assuming that custom, "home-grown" ML systems will be as easy or effective. There is a much different effort-to-outcome ratio for custom ML than there is using someone else's pre-trained model.
-
[Assuming] ML algorithms are trained more than once
Getting a trained ML algorithm to work on your laptop means you're around 10% of the way there. Production ML algorithms that are part of core business processes are trained many, many times. It is necessary to make that training process as easy and seamless as possible.
-
Trying to design your own perception or NLP algorithm
Josh warns that perception and NLP algorithms seem much easier to implement than they actually are. The production algorithms that currently exist for these types of systems are very highly-tuned from decades of academic research. Almost always use off the shelf solutions for these ML systems. The investment required to make one of these systems state-of-the-art is very high.
So those cautionary warnings are the pitfalls, but what is the good news?
“Most of the value comes along the way. As you march towards ML, you may not get there, and you will still greatly improve everything you’re working on. And if you do get there, ML improves almost everything it touches once you’re ready.” - Josh Cogan
Josh adds that ML can be a great differentiator. If investing in ML is difficult for your company, it is likely just as difficult for the other members of your industry. Once invested, however, ML will create a strategic advantage for your company that will be hard for other companies to duplicate or catch up to. This is because of the feedback loop inherent to Machine Learning; it gets better with time and data.
So despite the temptation to jump directly to a fully machine learned, automated, end-to-end system, Josh warns this is not the best path forward. The next sections discuss more realistic, higher-success-probability paths forward.
ML and Business Processes
Recall Josh’s premise: the value of ML “comes along the way.” This section documents a company’s path from no ML to having fully-machine-learned systems and processes.
In Josh’s words, this has to do with the evolution of business processes, where a business process is any activity that a company must do directly or indirectly to serve its customers. Organizations must improve these processes through feedback loops. Consider the example of a call center. Following a call to a customer support center, the consumer is often sent a survey. The results of these surveys are used to refine HR and training manuals, and may result in employee retraining. Ultimately, this creates changes to the processes by which the call center is run. This feedback enables operational expertise to be translated into better future outcomes.
The feedback loop Josh describes resembles the following image, recreated from a similar image Josh included as part of his presentation. It is representative of the class of all business processes.
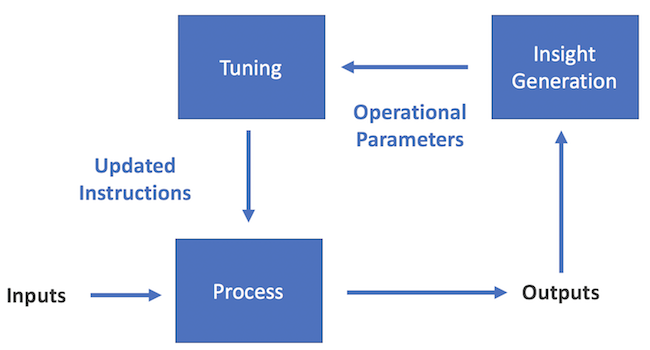
The path toward a full-machine-learned process involves automating each of these boxes. The phases of this path are defined as follows.
-
Individual Contributor
Process task is informally performed by a single person. An example is a receptionist.
-
Delegation
As task becomes more important and core to business processes, more people begin performing the same work. During this part of the process the work begins to become more formalized and repeatable. An example would be check-out clerks.
-
Digitization
The core repeatable part of a task becomes automated by a computer. An example is an ATM, which automates the more simplistic banking tasks.
-
Big Data and Analytics
At this phase, large amounts of data are used to create operational and business insights. Analytics can be applied to internal operations or to external users, which would be like advanced marketing research. An example is Toyota's lean manufacturing philosophy, where they measure many aspects of their processes to fine tune their operations.
-
Machine Learning
During this final phase, the tuning process itself is automated. The algorithm itself begins learning how to improve. An example is YouTube's recommendation engine.
The first three phases impact the business process itself, whereas analytics impacts the insight generation box, and machine learning impacts the tuning box, as shown below.
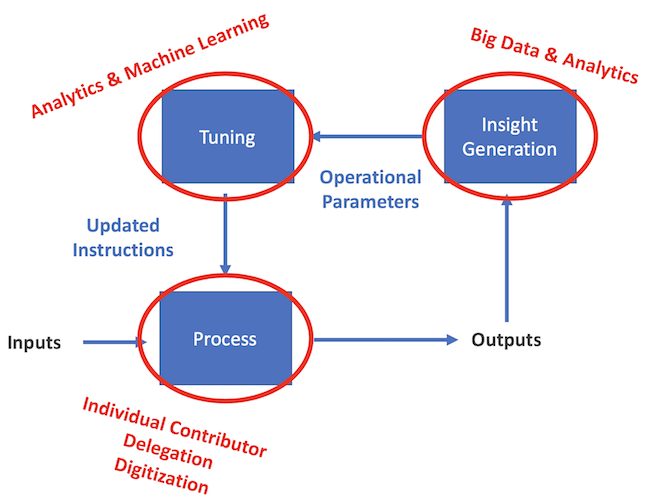
The Path to ML
This section is a deeper dive on the phases of process evolution outlined in the previous section. Each phase of this process presents both opportunities and risks, outlined below.
-
Individual Contributor
Opportunity: prototype and try out ideas
Dangers of skipping: inability to scale, product heads make incorrect assumptions that may be irreversible later
Dangers of lingering: highly-skilled individuals leave, failure to scale the process to meet demand
-
Delegation
Opportunity: gently ramp investment while maintaining flexibility to change
Dangers of skipping: Not forced to formalize process, diversity of human approaches become a testbed for possible improvements, great ML systems need humans in the loop
Dangers of lingering: Paying high marginal costs to serve each user, more voices and vested interests resist the progression toward automation, organizational inertial and lock-in
-
Digitization
Opportunity: Automate mundane parts of the process
Dangers of skipping: ML solutions require software infrastructure surrounding it, your IT project and ML success are tied together
Dangers of lingering: Competitors are collecting data and tuning offers from the insights being generated
-
Big Data and Analytics
Opportunity: Measure and achieve data-driven success
Dangers of skipping: Unclean data means no ML training, impossible to measure success of an ML system if there is no existing benchmark
Dangers of lingering: Limits the complexity of problems that your organization can solve
The dangers of staying at the big data and analytics phase are somewhat less than those associated with staying too long at the previous phases. As an example, Google search was a hand-tuned algorithm for much longer than most people realize, and it was very successful. The message is that organizations can get very far with more traditional analytics approaches, and without ceding total control to ML.
Google typically expects a 10% increase in the KPIs for a system that adopts machine learning, above and beyond the performance of hand-tuned algorithms. This is due to ML’s facility at handling myriad inputs and nuances. Ultimately this exceeds the limitations of human cognition.
End of Phases Deep Dive
| Ind. Contr. | Delegation | Digitization | Big Data | ML | |
|---|---|---|---|---|---|
| Who Executes? | One Person | Many People | Software | Software | Software |
| Operational Parameters? | Human Hypothesis | Human Hypothesis | Human Hypothesis | Data-Driven Insights | Data Regressions & Models |
| How does feedback work? | HR Training | HR Training | Software Engineer | Software Engineer | Machine-selected & Derived |
Final Reminders:
- Don’t leap into a fully-ML solution without completing the intervening steps outlined in this note. ML Success at Google typically follows a more structured approach that steadily increases the upfront investment as business uncertainties decrease with more research into the users and products niche. Your organization should follow the well-trod path outlined above.
- Google wants to help you with this. See cloud.google.com/training.
The specialization is sponsored by Google Cloud and this particular course is presented by Josh Cogan, a Software Engineer for Google AutoML.